Kol.1

1.Obliczyć wartości ciepeł molowych pod stałym ciśnieniem (T=298K)wszystkich substancji biorących udział w reakcji:

N_2(g) + 3H_2(g) = 2NH_3(g) +Q

oraz ΔC_p tej reakcji.

Rozw.

n- ilość moli w cząsteczce

l=0 - dla cząsteczek liniowych

l=1 - dla cząsteczek nieliniowych

C_p=C_v + R R=8,314 [kJ/mol·K]

N₂ - cząsteczka liniowa, n=2, l=0

H₂ - cząsteczka liniowa (C_p - jak wyżej)

NH₃ - cząsteczka nieliniowa, n=4, l=1

1b.Obliczyc wartości ciepeł molowych pod stałym ciśnieniem. (T=298K) wszystkich substancji biorących udział w reakcji N₂ +3H₂=2NH₃ oraz ΔCp tej reakcji.

2.Standardowa entalpia spalania gazowego propanu wynosi -2220 kJ/mol , a standardowa entalpia parowania ΔH_par ciekłego propanu 15 kJ/mol. Obliczyć wartość standardowej entalpii spalania i standardowej energii wewnętrznej spalania ciekłego propanu.

ROZW.

C₃H_8(g) + O₂ = CO₂ + H₂O ΔH=-2220 [kJ/mol]

C₃H_8(c) = C₃H_8(g) ΔH=15 [kJ/mol]

Po zsumowaniu:

C₃H_8(c) = CO₂ + H₂O ΔH=-2220+15=-2205 [kJ/mol]

2b. Standardowe entalpie tworzenia wody ,dwutlenku węgla, tlenku węgla wynoszą odpowiednio :

-285,9; -393,5; -110,5 [KJ/mol] a standardowa entalpie tworzenia metanu -74,8 kJ/mol. Obliczyć standardowe entalpie i energie wewnętrzna reakcji:

1) CH₄ + O₂ = C+ 2H₂0_(c)

2) CH₄+2O₂=CO₂+2H₂0_(c)

ROZW.

1)

2)

3.Standardowe entalpie tworzenia:

H₂O_(g) , CO_2(g) , CH₄ wynoszą:

-241,8 kJ, -393,5 kJ, -78,4 kJ

Obliczyć entalpie reakcji: CH_4(g)+2O₂=2H₂O + CO₂ w temp. 1500K i pod ciśnieniem 1 bar.

31,46 +0,00339T

30,00 +0,01071T

44,14 + 0,00904T

31,2 + 0,003T

Rozw.

CH_4(g)+2O₂=2H₂O_(g) + CO_2(g)

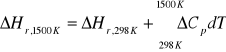
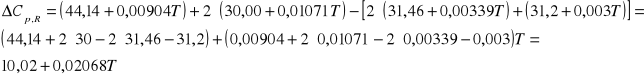
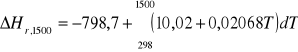
3b. Standardowa entalpia tworzenia gazowego amoniaku w temp.298K wynosi -46,2KJ/mol ciepła molowe wynoszą:

29,1 +0,002T

27,1+0,006T

25,9+0,032T

Obliczyć ΔH i ΔU dla reakcji powstawania gazowego amoniaku w temp.400K.

ROZW.

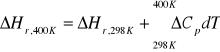
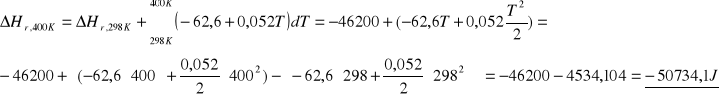
Kol.2

1.Stała równowagi reakcji Fe₃O_4(s) + CO = 3FeO_(s) + CO₂ przy 850K wynosi K_p=1,2 , mieszaninę złożoną z 1 mola Fe₃O₄ ; 1,5 mola CO ; 0,7 mola FeO; 0,4 mola CO₂ ogrzano do temperatury 850K przy całkowitym ciśnieniu 5 bar. Obliczyć ilość poszczególnych reagentów w stanie równowagi.

ROZW.

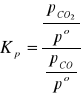
	Fe3O4(s)	CO	FeO(s)	CO2
Było[moli]	1	1,5	0,7	0,4
	Co-α	Co-α	Co+3α	Co+α
Jest[moli]	0,454545	0,954	2,3364	0,945

2.Obliczyć stałą równowagi K_p reakcji C_(s) + ½ O_2(g) =CO_(g) w temperaturze 1000K na podstawie danych:

K_p298=1,06·10²⁴

ΔH^o₂₉₈= -110,5 kJ/mol

Cp_(C)/[J/mol·K]=17,5 + 0,00427T

Cp_(O2) /[J/mol·K]=31,46 + 0,0034T

Cp_(CO) /[J/mol·K]=28,41 + 0,0041 T

ROZW.

średnia entalpia dla temperatury średniej:

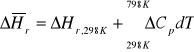
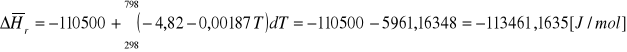
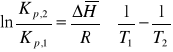
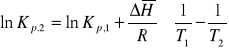
3. Prężność pary cieczy w zakresie temperatur 200-260K jest opisana przez : ln(p/Tor)=16,255-2501,8/T [K]

Tor=133,33Pa

Oblicz entalpię parowania tej cieczy.

Rozw.

1a. Oblicz stałą równowagi K_p w temperaturze 298K dla następującej reakcji

CO_2(g) + 2H_2(g) = CH₃OH_(g). Wiedząc ,że standardowa zmiana potencjału termodynamicznego dla reakcji: CO_2(g) + 2H₂ = CH₃OH_(c)

a prężność pary metanolu w temperaturze 298K wynosi: 16,2 kPa.

ROZW.

CO_2(g) + 2H_2(g) = CH₃OH_(c)

CH₃OH_(c)= CH₃OH_(g).

p=16200Pa

p^o=100000Pa

2a. Dla reakcji syntezy acetylenu 2C_(s) + H_2(g) =C₂H_2(g) w zakresie temperatur 700-1500K i przy ciśnieniu 1 bar, standardowa entalpia reakcji jest funkcją temperatury:

Obliczyć wartość stałej równowagi K_p,2 w temperaturze 1500K, jeżeli w temperaturze 700K K_p,1=7,94·10¹³.

ROZW.

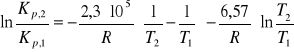
3a. Dla reakcji: 3Fe₂O₃ = 2Fe₃O₄ + ½ O_{2 ,}

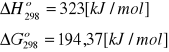
Oblicz stałą równowagi K_p tej reakcji:

a) 298K

2. 478K.

ROZW.

a)

b)

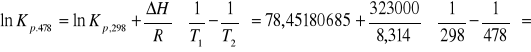
127,5449509

4a. Stała równowagi reakcji syntezy amoniaku NH₂ + 3H₂ = 2NH₃ w temperaturze 400K wynosi K_p,1=1,26·10 ^-7 . Obliczyć stałą równowagi K_p,2 , w temperaturze 500K jeżeli w podanym zakresie temperatur standardowa entalpia reakcji:
.

ROZW.

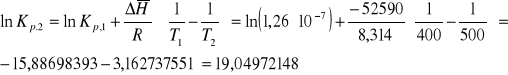
4.1/str. 41 skrypt

4.4/str. 43 skrypt

4.6/str. 45 skrypt

4.8/str. 47 skrypt

5a. Stała równowagi reakcji H₂ + Cl₂ = 2HCl można wyrazić równaniem:
. Znaleźć standardowe entalpie tej reakcji dla temperatury 1000 K.

ROZW.

6a.W temperaturze 1000K i pod ciśnieniem 1 bar z mieszaniny zawierającej początkowo 1 mol SO₂ ; 0,6 moli O₂ w trakcie ustalania się równowagi powstało 0,22 moli SO₃. Wyznaczyć stałą równowagi ciśnieniowej K_p reakcji. 2SO₂ + O₂ = 2 SO₃

ROZW.

	SO2	O2	SO3.
było	1	0,6	-
	1- α	0,6- α/2	α
jest	0,78	0,49	0,22

Σn=1,49 moli

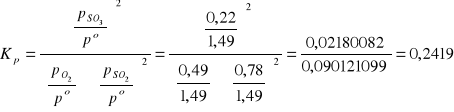
Kol. 3

1.Prężności par substancji A i B w temp. 323K wynoszą odpowiednio 0,0467 i 0,1 MPa. Obliczyć całkowitą prężność i skład pary pozostającej w równowadze z roztworem składającym się z 5 moli substancji A i & moli substancji B (roztw. doskonały).

Rozw.

n_A=5 moli

n_B=7 moli

p^o_A=0,0467 MPa=46700 Pa

p^o_B=0,1 MPa=100000 Pa

x_A=
x_B=1-x_A

x_B=

p_A= x_A· p^o_A=19458,333 Pa

p_B= x_B · p^o_B=58333,333 Pa

p =p_A +p_B=77791,666 Pa

Skład pary:

y_A=
y_B=1-y_A

y_B=

1b. Obliczyć aktywność i współczynnik aktywności eteru w mieszaninie z etanolem wiedząc, że jego ułamek molowy w roztworze wynosi 0,6 a w parze 0,75.

Całkowite ciśnienie nad roztworem wynosi 3,6·10⁴Pa. A prężność pary nad czystym eterem jest równa 3,87·10 ⁴Pa.

2.Obliczyć temperaturę wrzenia roztworu otrzymanego po rozpuszczeniu 0,8 g naftalenu(n) w 50g chloroformu(ch).

Temperatura wrzenia chloroformu wynosi T_wrz=61,1^oC. Molowa entalpia parowania ΔH_p=29,37 [kJ/mol].

Masy molowe: M_ch=119,4 g/mol

M_n=128,2 g/mol

Rozw.

m_n=0,8 g rozpszczono w 50 g chloroformu.

T_{wrz ,ch}=61,1 ^oC=334,25 K

ΔH_p=29,37 [kJ/mol]=29370 [J/mol]

ΔT_wrz=K_e · m m [mol/1000 g _rozp]

n_n=

0,006240249 mole_n — 50 g _ch

x moli_n — 1000 g _ch

x=0,1248 moli_n molalność:0,1248 [moli/kg _rozp]

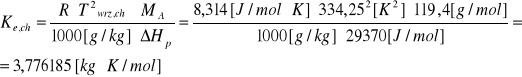
M_A=M_ch - masa cząsteczkowa rozpuszczalnika,

ΔT_wrz=3,776185 · 0,1248 = 0,47126 K

ΔT_wrz,R= T_{wrz ,ch}+ ΔT_wrz = 334,7212 K.

2b. W 100kg wody rozpuszczono 3,7488g substancji.

Temp. wrzenia tego roztworu była wyższa od temp wrzenia rozpuszczalnika o ΔT=0,2107K.

Obliczyć masę molową substancji rozpuszczonej wiedząc ,że był nią siarczan sodowy .

Obliczyć współczynnik izotoniczny i, Ke=lub wody 0,512[ kg· K/mol]

ROZW.

3.Obliczyć wielkość nadmiaru powierzchniowego Γ₂ etanolu w roztworze wodnym o C=0,5 [mol/dm³] w temperaturze 298K wiedząc, że zależność napięcia powierzchniowego roztworu od stężenia przedstawia równanie empiryczne:

0,072 -0,5·10 ^{- 4}C +0,2 ·10 ^-7C²

ROZW.

-0,5·10 ^{- 4} +2·0,2·10 ^-7 C

C=0,5 mol/dm³=500 mol/m³

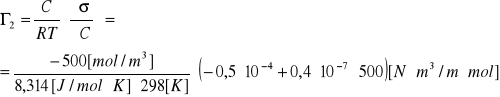
Γ₂=0,000006054= 6,054·10 ^-6[mol/m³]

3b.
0,073-1,09·10 ^-4 +1,07·10^-7 c²

Kol.4

1.Roztwór zawierający 0,025 mola Na₂SO₄ w 100 g wody poddano elektrolizie w aparacie Hittorfa. Na anodzie przebiegła reakcja: 2H₂O = 4 H⁺ + O₂ +4e^- po zakończeniu elektrolizy przestrzeń anodowa zawierała 100 g H₂O i 0,01 mola jonów H⁺, które oznaczono przez
miareczkowanie, t_Na+=0,390. Określić liczbę moli jonów Na⁺ , SO₃ ^{2 -} po zakończeniu doświadczenia. M_Na=23g/mol , M_S=32g/mol.

2.Korzystając z równania Hickla-Debaya obliczyć średni współczynnik aktywności jonów , oraz aktywność elektrolitu roztworze wodnym Al₂(SO₄)₃ o stężeniu m=0,02 mol/kg

A=0,509 , a·B=1 , a₂=?

ROZW.

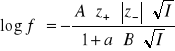
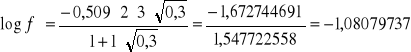
3.Standardowa siła elektromotoryczna ogniwa:

Pt, H_2(g)│HCl_aq│AgCl_(s),Ag_(g)

Zależy od temperatury w następujący sposób: E^o=0,2224-6,4 · 10 ^-4(T-298) [V]

Obliczyć: ΔG^o, ΔH^o, K_a reakcji zachodzącej w tym ogniwie oraz silę elektromotoryczną w temperaturze 328K

ROZW.

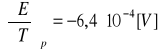
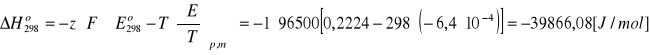
Kol.5

1.Reakcja rozkładu nadtlenku wodoru przebiega zgodnie z równaniem:

H₂O₂=H₂O +1/2 O₂

Kinetykę tej reakcji badano miareczkując za pomocą roztworu KMnO₄ próbki o jednakowej objętości (5cm³) pobierane co pewien czas. Otrzymano następujące wyniki:

t [min]	127	135	141	148
V[cm^3]	9,50	7,01	5,58	4,28

Wyznaczyć rząd i stałą szybkości reakcji.

ROZW.

Metoda różnicowa Van't Hoffa.

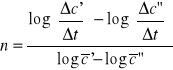
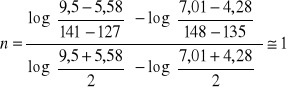
Dla reakcji I rzędu:

zatem:

2Stała szybkości reakcji : CH₃COOH₃ +NaOH =CH₃COONa +CH₃OH ,

wynosi 4,9 [dm³/mol·min] w temperaturze 293K. Obliczyć jaki procent estru ulegnie zmydleniu w tej temperaturze po 8-miu minutach, jeżeli początkowe stężenie estru i zasady są jednakowe i wynoszą 0,03 [mol/dm³].

ROZW.

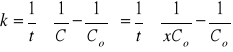
zostało: 46%

przereagowało:54%

3. Zależność stałej szybkości reakcji rozkładu arsenowodoru AsH₃ od temperatury, w zakresie 500-1000K, przedstawia równanie:

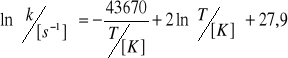
Wyznaczyć zależność energii aktywacji od temperatury oraz energię aktywacji w temperaturze 800K.

po zlogarytmowaniu:

po zróżniczkowaniu:

pochodna równania

[J/mol]=3,24246[MJ/mol]

4.Reakcja pierwszego rzędu: A→produkt , ustalono ze po jednej godzinie A/A_o = 0,125.Początkowo w układzie znajdowało się 0,2 mola gazu A (warunki normalne). Wyznaczyć czas połowicznego przereagowania oraz początkową szybkość reakcji.

ROZW.

5.Okres połowicznego rozpadu reakcji I-rzedu wynosi :

τ₁=100 min przy T=323K,

τ₂=15 min przy T=353K.

Obliczyć E_a.

ROZW.

Równanie Arrheniusa:
po scałkowaniu: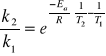
i po zlogarytmowaniu: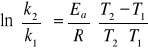

o

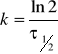
, lub:

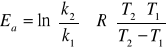
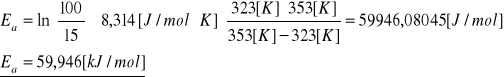
6.Po 800 s przereagowała połowa początkowej ilość substancji. Jaka część po 1100s ?

1. dla reakcji I rzędu,

2. dla reakcji II rzędu.

ROZW.

a)

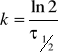
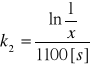
zostało:38,55%

przereagowało:61,45%

b)

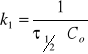
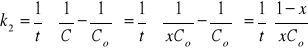
zostało: 36,347%

przereagowało: 64,63%

7. A+B→produkty, T=298K

Wyjściowe jednostkowe stężenie produktów:

t	0	30	60	180	360
C	0,05	0,0485	0,0472	0,0426	0,0386

Wyznaczyć rząd i stałą szybkości reakcji.

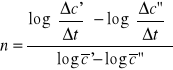
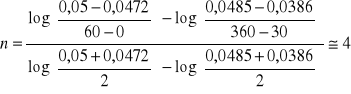
(1/3-2/5)

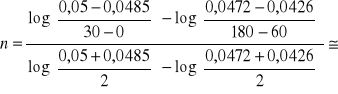
2,8 (1/2-3/4)

18

---