Nr ćwiczenia: 9	Temat ćwiczenia: Współczynnik załamania światła dla ciał stałych	Ocenia z teorii:
Nr zespołu: 6	Imię i nazwisko: Mateusz Knapik	Ocena z zal. ćwiczenia:
Data: 19.03.2007r.	Wydział: EAIiE Rok: I Grupa: 2	Uwagi:

I. Cel ćwiczenia:

Wyznaczenie współczynnika załamania światła dla ciał stałych metodą mikroskopu.

II. Wstęp teoretyczny:

Współczynnik załamania jest to stosunek prędkości światła w próżni do prędkość światła w

danym ośrodku.

Zasada Huygensa mówi, iż każdy punkt ośrodka, do którego dotarło czoło fali można uważać za źródło nowej fali kulistej. Fale te zwane są falami cząstkowymi i interferują ze sobą. Wypadkową powierzchnię falową tworzy powierzchnia styczna do wszystkich powierzchni fal cząstkowych i ją właśnie obserwujemy w ośrodku.

Prawo odbicia: Promień padający, odbity i normalna do powierzchni odbicia są współpłaszczyznowe. Dodatkowo, kąt padania jest równy kątowi odbicia.

Prawo załamania: Stosunek sinusów kątów padania i załamania jest równy stosunkowi prędkości światła w każdym z tych ośrodków. Z tego wynika, iż stosunek bezwzględnego współczynnika załamania ośrodka drugiego n2 do bezwzględnego współczynnika załamania ośrodka pierwszego n1, jest równy współczynnikowi względnemu załamania światła ośrodka drugiego względem pierwszego.

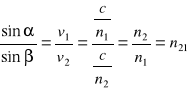
Całkowite wewnętrzne odbicie to zjawisko fizyczne zachodzące dla fal (najbardziej znane dla światła) występujące na granicy ośrodków o różnych współczynnikach załamania. Polega ono na tym, że światło padające na granicę od strony ośrodka o wyższym współczynniku załamania pod kątem większym niż kąt graniczny, nie przechodzi do drugiego ośrodka lecz ulega całkowitemu odbiciu.

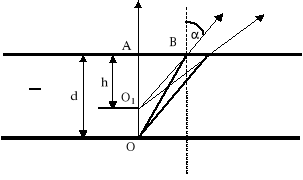
Wskutek załamania światła odległości przedmiotów umieszczonych w środowisku optycznie gęstszym obserwowane z powietrza wydają się mniejsze. Szyba sprawia wrażenie cieńszej, niż jest w rzeczywistości, przedmioty w wodzie wydają się bliższe powierzchni itd. Zjawisko to można prześledzić analizując bieg promienia w płytce płaskorównoległej.

Promień OA prostopadły do powierzchni granicznej wychodzi bez załamania, natomiast OB tworzy z normalną wewnątrz szkła kąt , a w powietrzu kąt , większy od  wskutek załamania. Obserwowane promienie wychodzące z płytki są rozbieżne, ich przedłużenia przecinają się w punkcie O_1­ tworząc obraz pozorny. Odległość O₁A równa h stanowi pozorną grubość płytki, podczas, gdy AO = d jest grubością rzeczywistą.

Dyspersja - w optyce to zależność współczynnika załamania n ośrodka (np. szkła) od długości fali. W efekcie światło o różnych długościach załamane np. na pryzmacie załamuje się pod różnymi kątami, co daje rozdzielenie światła białego na barwy tęczy zwanego rozszczepieniem światła. Zależność współczynnika załamania światła od długości fali światła nazywana jest współczynnikiem dyspersji i jest parametrem określającym własności minerałów.

Dyspersja współczynnika załamania to zależność tego współczynnika od długości fali.

Dyspersja normalna - wzrost współczynnika załamania wraz ze wzrostem częstotliwości

Dyspersja anomalna - współczynnik załamania maleje wraz ze wzrostem częstotliwości

Mikroskop jest to przyrząd złożony z dwóch soczewek - obiektywu i okularu, znajdujących się na wspólnej osi optycznej w pewnej odległości od siebie. Obie te soczewki muszą mieć krótkie ogniskowe, a zatem w rzeczywistych układach mikroskopów nie mogą to być pojedyncze cienkie soczewki, lecz odpowiednio wykonane układy soczewek, w których aberracja sferyczna i chromatyczna oraz astygmatyzm zostały zmniejszone do minimum. Powiększenie mikroskopu jest iloczynem powiększeń obiektywu i okularu.

Powstawanie obrazu w mikroskopie.

III. Wyposażenie stanowiska

W doświadczeniu współczynnik załamania wyznacza się z porównania grubości rzeczywistej z grubością pozorną. Do pomiaru grubości rzeczywistej korzysta się ze śruby mikrometrycznej. Do pomiaru grubości pozornej wykorzystuje się mikroskop zaopatrzony w czujnik położenia do określania wielkości przesuwu obiektywu mikroskopu. Elementami dla których określany jest współczynnik załamania są płasko-równoległe, przezroczyste płytki szkła i pleksiglasu.

IV. Wykonanie pomiaru

1. Zmierzyć śrubą mikrometryczną grubość rzeczywistą płytek. Pomiar wykonać kilkakrotnie.

2. Narysować flamastrem na każdej z powierzchni płytki linię tak, by linie te się krzyżowały. Linie te mają służyć do łatwiejszego ustawienia ostrości górnej i dolnej powierzchni płytki w mikroskopie i do identyfikacji powierzchni.

3. Po umieszczeniu płytki na stoliku mikroskopu ustawić na ostrość obraz linii na jednej z powierzchni płytki. Odczytać wskazanie czujnika.

4. Ustawić na ostrość obraz linii na drugiej powierzchni i dokonać odczytu czujnika.

5. Czynności z punktów 3 i 4 powtórzyć dziesięciokrotnie.

6. Wyniki zapisywać w tabeli:

Płytka	D	d1	d2	d1	d2	d1-d2	N
		grubość rzeczywista	górna powierzchnia	dolna powierzchnia	średnia arytmetyczna	średnia arytmetyczna	grubość pozorna	współczynnik załamania

5. Opracowanie wyników:

1. Obliczenie wartości średnich wskazań czujnika przy ustawieniach mikroskopu na ostrość górnej i dolnej powierzchni i zapisanie wyników w tabeli.

2. Obliczenie grubości pozornej płytek (
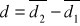
   ), a następnie współczynnika załamania - stosunek grubości rzeczywistej zmierzonej śrubą mikrometryczną i grubości pozornej (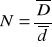
   ). Zapisanie wyników do tabeli.

3. Aby obliczyć błąd średni kwadratowy wartości średniej odczytu wskazania czujnika dla powierzchni górnej i dolnej posłużę się wzorem:
   .

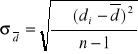
Ponieważ grubość pozorna płytki zależy od zmierzonych wartości
i
oraz brania pod uwagę średniego odchylenia wartości średniej, w celu wyznaczenia błędu tej grubości posłużę się prawem przenoszenia błędów na mocy którego: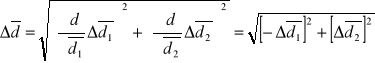

, gdzie

Wyniki dokonanych obliczeń w tym punkcie zestawiono w poniższej tabeli:

Płytka
duża prostokątna	0,03 mm	0,04 mm	0,05 mm
okrągła	0,02 mm	0,02 mm	0,03 mm
kwadratowa	0,02 mm	0,02 mm	0,03 mm
mała prostokątna	0,02 mm	0,02 mm	0,02 mm

4. W celu obliczenia błędu wyznaczenia współczynnika załamania posłużę się metodą pochodnej logarytmicznej. Współczynnik ten został obliczony na podstawie wzoru:
   .

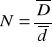
Po logarytmowaniu obu stron równania otrzymujemy
, a po zróżniczkowaniu:
. Po zastąpieniu przyrostów maksymalnymi błędami oraz zamianie różnicy błędów na sumę (wynika to z faktu, iż chcemy obliczyć największy błąd) ostatecznie otrzymujemy wzór na błąd współczynnika załamania: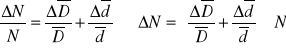

Błąd bezwzględny wyznaczenia grubości rzeczywistej wynika z dokładności odczytu śruby mikrometrycznej czyli ΔD=0,01mm.

Wyniki dokonanych obliczeń w tym punkcie zestawiono w poniższej tabeli:

Płytka	N	ΔN
duża prostokątna	1,492	0,028
okrągła	1,527	0,018
kwadratowa	1,462	0,025
mała prostokątna	1,518	0,032

5. 
   Istnieje możliwość wyznaczenia zależności współczynnika załamania światła od długości fali N(λ), czyli tzw. dyspersji. Aby tego dokonać na płytkę musiałoby padać światło monochromatyczne. Wiemy, iż dla każdej barwy światło ma inną długość fali.

Jeśli dla różnych barw dokonalibyśmy serii pomiarów takich jak podczas doświadczenia wówczas po zebraniu wyników w postaci charakterystyki N(λ) moglibyśmy otrzymać wykres np. takiej postaci:

Należy jedynie zwrócić uwagę, iż na wykresie powyższym zależność N(λ) została także przedstawiona dla światła ultrafioletowego i podczerwonego.

Z wykresu widać, że dla malejącej długości fali rośnie współczynnik załamania dlatego dyspersja w przypadku szkła jest dyspersją normalną.

6. Wnioski końcowe:

Na podstawie przeprowadzonego doświadczenia i dokonanych obliczeń można stwierdzić, że najdokładniejsze pomiary stosując tę metodę można otrzymać dla cieńszych płytek (grubość rzeczywista), wówczas pozorny błąd grubości płytki jest najmniejszy. Należy też zwrócić uwagę, iż podczas pomiaru grubości pozornej największy udział w błędzie wyznaczania współczynnika załamania, nie miała dokładność odczytu z przyrządu zegarowego, lecz ustawienie ostrego obrazu powierzchni płytek.

Uzupełnienie sprawozdania:

Tabela z pkt. 3 opracowania:

Płytka
PLEKISGLAS duża prostokątna	0,03 mm	0,04 mm	0,05 mm
SZKŁO okrągła	0,02 mm	0,02 mm	0,03 mm
PLEKSIGLAS kwadratowa	0,02 mm	0,02 mm	0,03 mm
SZKŁO mała prostokątna	0,02 mm	0,02 mm	0,02 mm

Tabela z pkt. 4 opracowania:

Płytka	N	ΔN
PLEKISGLAS duża prostokątna	1,492	0,028
SZKŁO okrągła	1,527	0,018
PLEKSIGLAS kwadratowa	1,462	0,025
SZKŁO mała prostokątna	1,518	0,032

Zestawienie wyników wyznaczenia współczynnika załamania z wartościami tablicowymi:

	DOŚWIADCZENIE	TABLICE FIZYCZNE
SZKŁO	1,523 ±0,025	1,52
PLEKSIGLAS	1,477 ±0,027	1,46

W powyższej tabeli dokonano uśrednienia wielkości współczynnika załamania i błędu jego wyznaczenia.

Uzupełnienie wniosków:

Po dokonaniu zestawienia wyników otrzymanych w doświadczeniu z danymi tablicowymi, okazało się, iż wyznaczone przez nas wartości współczynnika załamania są zbliżone do wartości tablicowych. Różnice są mniejsze od błędów pomiarowych, co świadczy o tym, że zaproponowana metoda wyznaczenia współczynnika załamania światła okazała się dokładna.

promień padający

promień odbity

kąt

padania

kąt

odbicia

normalna

kąt

padania

kąt

załamania

v₁

n₁

v₂

n₂

α

β

400 nm

700 nm

---