Szanowni Uczniowie!

Zapewne dobrze są Wam znane jedne z najprostszych i najważniejszych pojęć geometrycznych: cięciwa okręgu (koła), styczna do okręgu i sieczna okręgu. Ze względu na swoją prostotę i przejrzystość są one intuicyjnie łatwe do zrozumienia i nawet uczeń o przeciętnych uzdolnieniach matematycznych może bez problemu podać ich określenie, zwłaszcza, jeżeli wykona odpowiedni rysunek pomocniczy. Jednak w matematyce samo pojęcie, nawet najprostsze, jest pojęciem martwym, jeżeli nie jest ono powiązane z pewną nadbudową teoretyczną, zawierającą tematy i twierdzenia opisujące jego pojęcia z innymi pojęciami matematycznymi. W dydaktyce matematyki nadbudowę taką nazywamy teorią formalną, choć w odniesieniu do cięciw, stycznych i siecznych słowo teoria jest nieco przesadne. Dopiero wtedy pojęcie takie dla matematyka w pełni użyteczne, gdyż pozwala mu ono na rozwiązanie różnych ciekawych pożytecznych. Bywa, że przy okazji poszukiwania rozwiązania jakiegoś problemu definiowane są inne, nowe pojęcia. Analizując szkolne programy nauczania matematyki jakie obowiązywały w polskim szkolnictwie na przestrzeni ostatnich kilkudziesięciu lat trudno się w nich doszukać twierdzeń opisujących własności cięciw, stycznych i siecznych. Same te pojęcia, owszem bywały w programach nauczania, ale postulowano jedynie definicje tych pojęć i twierdzenie o odległości prostej od środka okręgu i jej stosunku do długości promienia okręgu. Własności cięciw, stycznych i siecznych trudno również znaleźć w podręcznikach do matematyki, dostosowanych do realizacji tych programów. Skutkiem tego w podręcznikach do matematyki oferowanych przez różne wydawnictwa szkolne jako pomoc dydaktyczna dla uczniów brak jest ciekawych i inspirujących zadań o cięciwach, stycznych i siecznych. Z obowiązującej obecnie podstawy programowej matematyki z treści odnoszących się do poziomu rozszerzonego wynika, że począwszy od roku 2010 na egzaminie maturalnym z matematyki uczeń ma się wykazać umiejętnością rozwiązywania zadań wymagających znajomości twierdzeń o związkach miarowych pomiędzy odcinkami cięciw, stycznych i siecznych. Stawia to przed nauczycielami matematyki szkół średnich obowiązek przygotowania Was do spełnienia tego wymagania. Spodziewajcie się więc drodzy uczniowie, że w niedalekiej przyszłości na lekcjach matematyki będziecie ze swoim nauczycielem przerabiać tego typu zadania. Wy również, chcąc dobrze i sprawnie rozwiązywać tego typu zadania powinniście sami je rozwiązywać (naprawdę warto). Artykuł ten nie pretenduje ani do oryginalności ani do naukowego rozumu. Nie ma w nim bowiem nic nowego czy odkrywczego. O stycznych, siecznych i cięciwach oraz ich własnościach mamy już wiedzę od czasów starożytnych. Notabene jedno z podanych poniżej twierdzeń jest nazywane czasami twierdzeniem Euklidesa. Artykuł jest jedynie próbą wyjścia naprzeciwko oczekiwaniom uczniów i nauczycieli, którzy w procesie nauczania - uczenia się stanęli przed koniecznością rozwiązywania zadań wymagających zastosowania twierdzeń o cięciwach, stycznych i siecznych. Jak już wspomniałem, w podręcznikach szkolnych do matematyki dostosowanych do realizacji nowej podstawy programowej znajdzie się odpowiedni materiał teoretyczny i pewna liczba zadań z tego tematu. Niewątpliwie zaletą tego artykułu jest duża liczba podanych zadań - po części rozwiązanych, po części przeznaczonych do samodzielnego rozwiązania. Autor artykułu dysponuje rzadkim (być może unikatowym) starym, prawie sześćdziesięcioletnim zbiorem tłumaczonym z języka rosyjskiego, w którym zadań tłumaczonym z języka rosyjskiego, w którym zadań tego typu (w porównaniu do innych podręczników) jest bardzo dużo. Część z nich jest bardzo oryginalna, niektóre są trudne i inspirujące. Wszyscy, którzy są zainteresowani tym artykułem i będą przerabiać zawarte w nim zadania w razie jakichkolwiek wątpliwości czy nieradzenia sobie z zadaniami są proszeni o kontakt z autorem artykułu.

Własności stycznych, siecznych i cięciw

Do rozwiązania poniższych zadań potrzebna jest znajomość pojęć: sieczna i styczna do okręgu i cięciwa okręgu. Zakładam, że czytelnik zna te pojęcia lub przypomni sobie je we własnym zakresie. Jednak znacznie bardziej przydatna będzie znajomość (najlepiej wraz z dowodem) twierdzeń wyrażających własności tych pojęć. Twierdzenia te są nazywane twierdzami o związkach miarowych odcinków cięciw, stycznej i siecznej. Materiał ten można znaleźć na przykład w starym podręczniku I. Iwaszkiewicza „Geometria elementarna”- część I, gdzie jest wyłożony w sposób bardzo przystępny.

Własność 1.

Promień okręgu poprowadzony do punktu styczności okręgu z prostą, tworzy z tą prostą kąt prosty.

Własność 2.

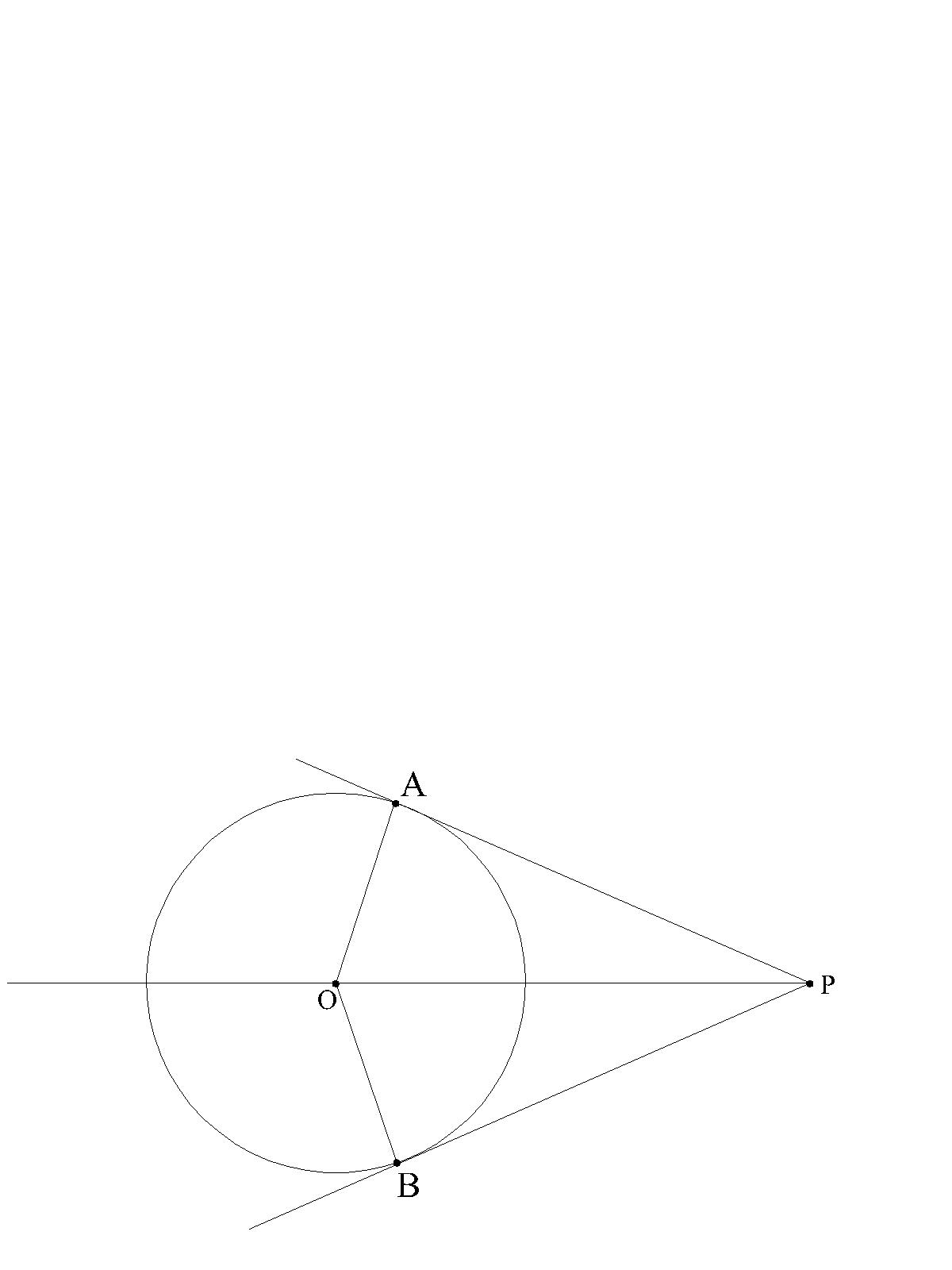
Jeżeli z danego punktu zewnętrznego poprowadzono do okręgu dwie styczne, to odcinki, których jednym końcem jest ten punkt, a drugim punkt styczności mają jednakową długość.

|AP|=|BP|

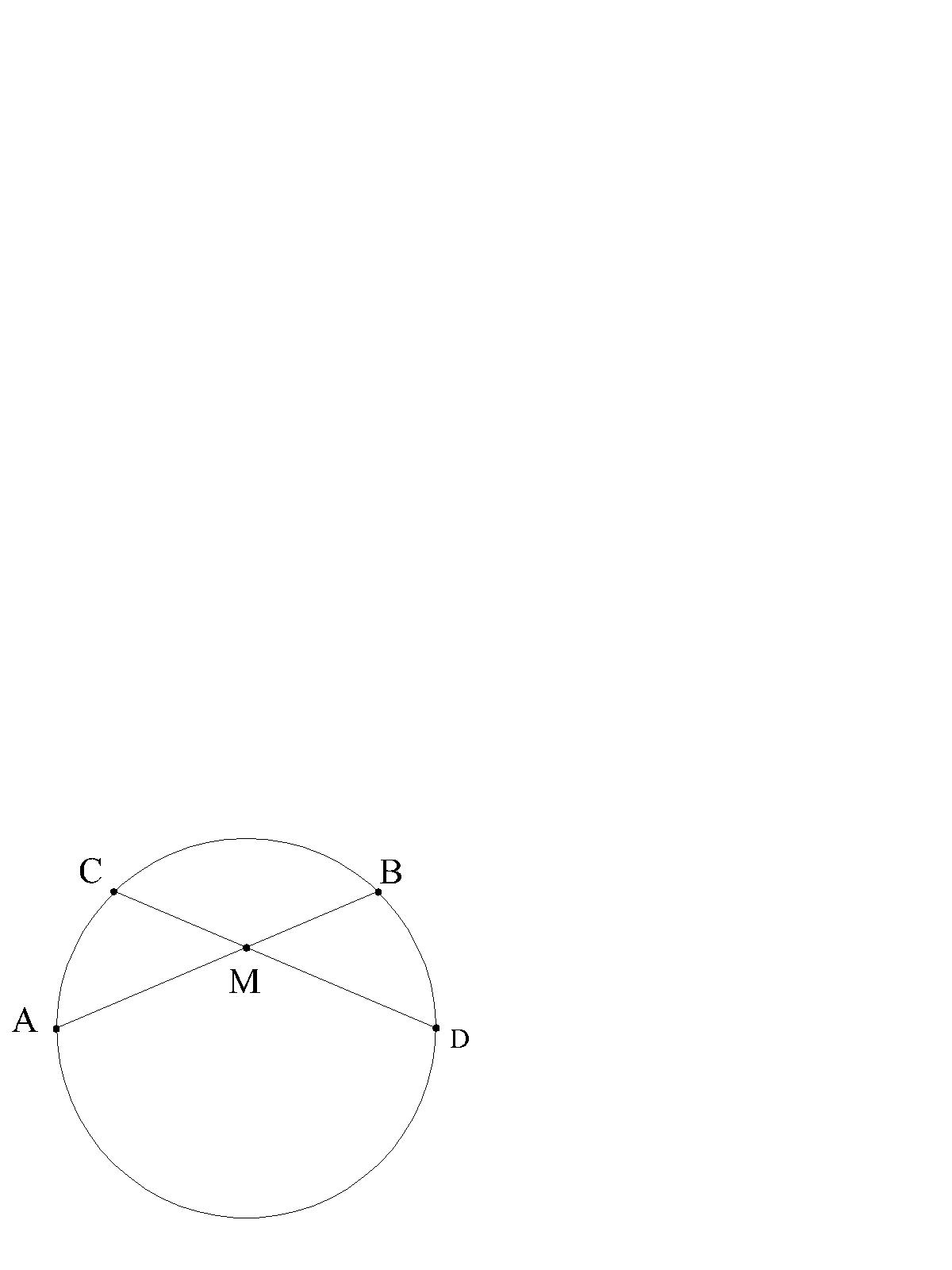
TWIERDZENIE 1. - O związkach miarowych odcinków przecinających się cięciw w okręgu (kole). Jeżeli cięciwy okręgu przecinają się w punkcie leżącym wewnątrz okręgu, to iloczyn odcinków każdej cięciwy, zawartych pomiędzy tym punktem i punktami przecięcia z okręgiem jest stały.

|AM|∙|BM|=|CM|∙|DM|

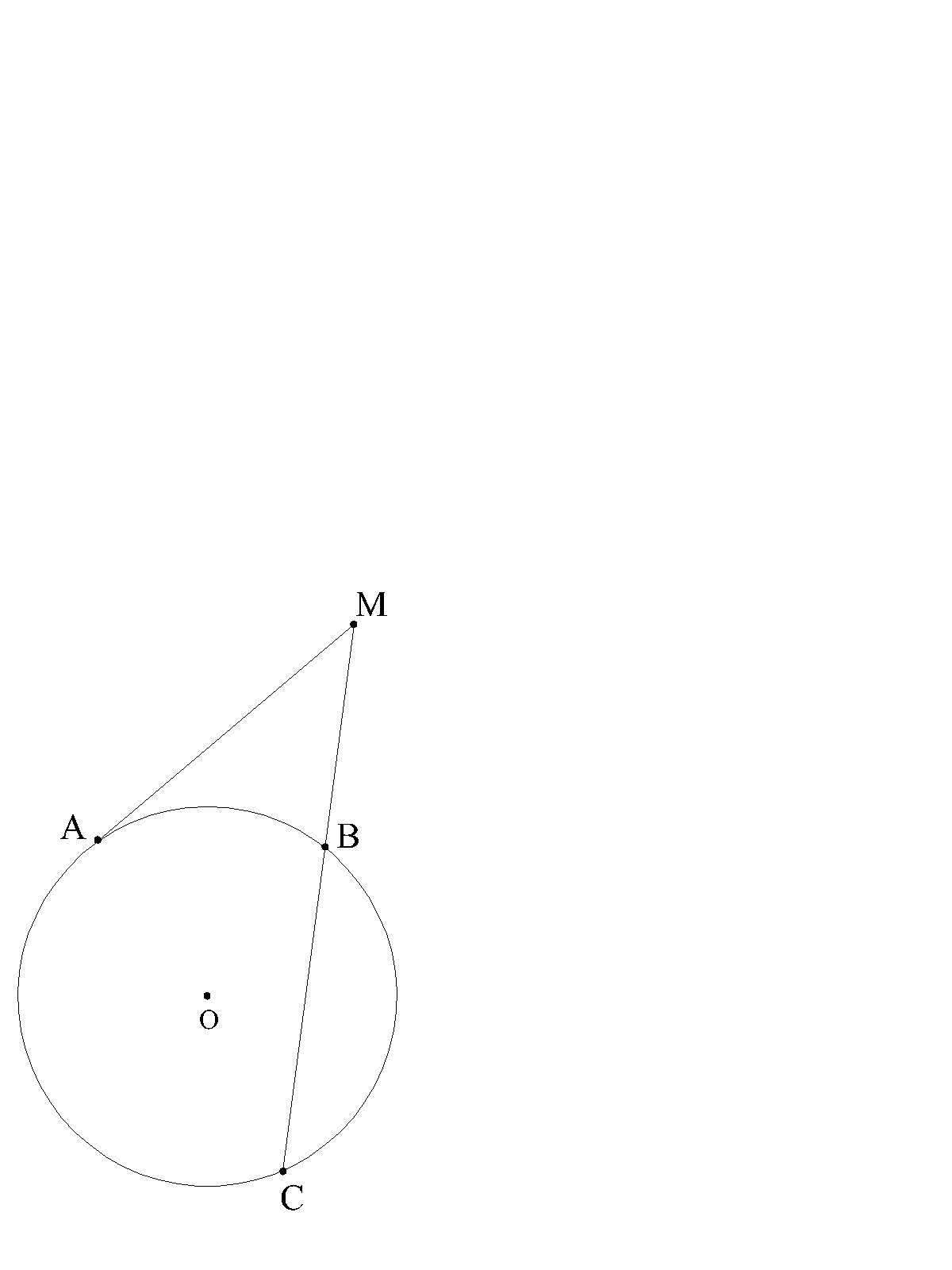
TWIERDZENIE 2.(Euklidesa) - O stycznej i siecznej. Jeżeli przez zewnętrzny okręgu poprowadzimy styczną i sieczną, to odcinek stycznej zawarty pomiędzy tym punktem i punktem styczności jest średnio proporcjonalny między odcinkami siecznej zawartymi pomiędzy danym punktem i punktem przecięcia siecznej z okręgiem.

|MA|²=|MB|∙|MC|

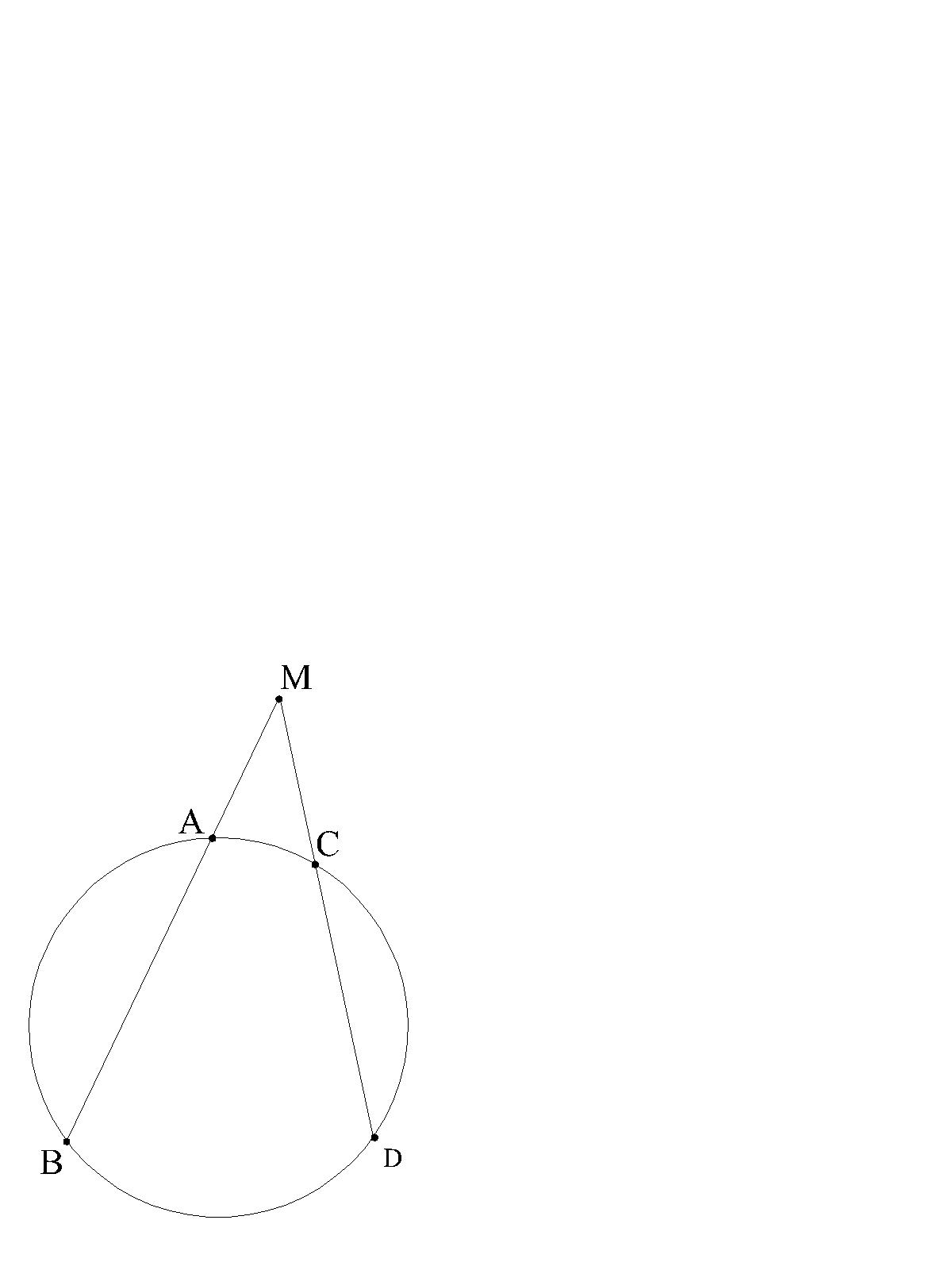
TWIERDZENIE 3.(O odcinkach siecznych) Jeżeli sieczne okręgu przecinają się w punkcie leżącym na zewnątrz tego okręgu, to iloczyn odcinków każdej siecznej zawartych pomiędzy tym punktem i punktem styczności jest stały.

|MB|∙|MA|=|MD|∙|MC|

TWIERDZENIE 4. (O kącie pomiędzy cięciwą, a styczną) Kąt ostry między cięciwą, a styczną do okręgu przechodzącą przez koniec cięciwy jest równy połowie kąta środkowego odpowiadającego tej cięciwie.

Szanowni uczniowie

Po zapoznaniu się z podanymi twierdzeniami, po ich przemyśleniu macie poniżej rozwiązanych 20 zadań na zastosowanie tych twierdzeń. Proponuję najpierw dokładnie przeczytać treść i prześledzić jego rozwiązanie. Najlepiej aktywnie, wykonując na papierze stosowane uzupełnienia rozwiązania.

Powodzenia.

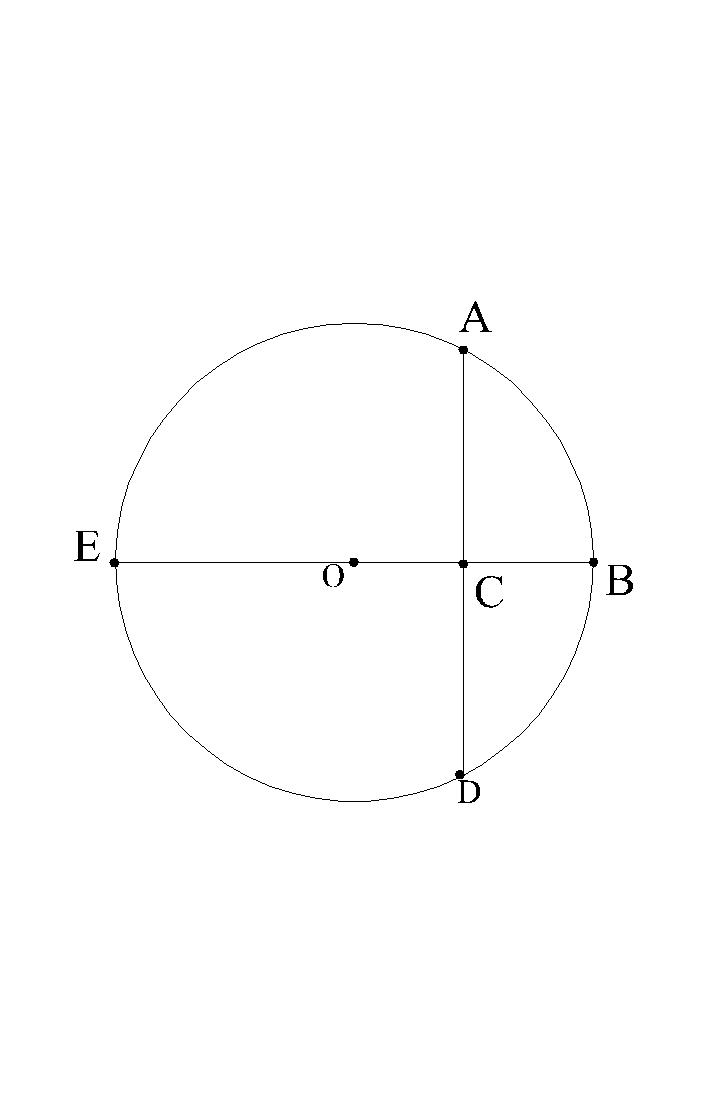
Zadanie 1. Z punktu A leżącego na okręgu o środku O i promieniu r=68 cm poprowadzono prostopadłą do promienia OB okręgu,dzielącą ten promień na odcinki OC i CB takie,że |OC| : |CB|=8:9. Obliczyć długość odcinka AC.

Dane: Rozwiązanie: Szukane :

r= |OB|=68 cm |AC|=?

Mamy:

|OC|+|CB|= |OB|=r=68 i

Z układu równań: |OC|+|CB|= |OB|=r=68 i
wyznaczamy: |OC|=32 i |CB|=36 Z twierdzenia o przecinających się cięciwach okręgu mamy |AC|² =|EC|∙ |CB|, gdzie |EC|=|EO|+|OC|=r+|OC|=68+32=100 |AC|² =100∙ 36 |AC|² =3600 i |AC|>0 |AC|=60

Odp: |AC|=60 cm.

Zadanie 2.Dwie cięciwy przecinają się wewnątrz okręgu tak, że odcinki jednej z nich mają długość 8 cm i 6 cm, a odcinki drugiej pozostają w stosunku 2:3. Obliczyć długości odcinków A drugiej cięciwy.

Dane: Rozwiązanie: Szukane : |AP|=6 cm |PD|=?

|PB|=8 cm |CP|=?

|CP|: |PD|=2:3

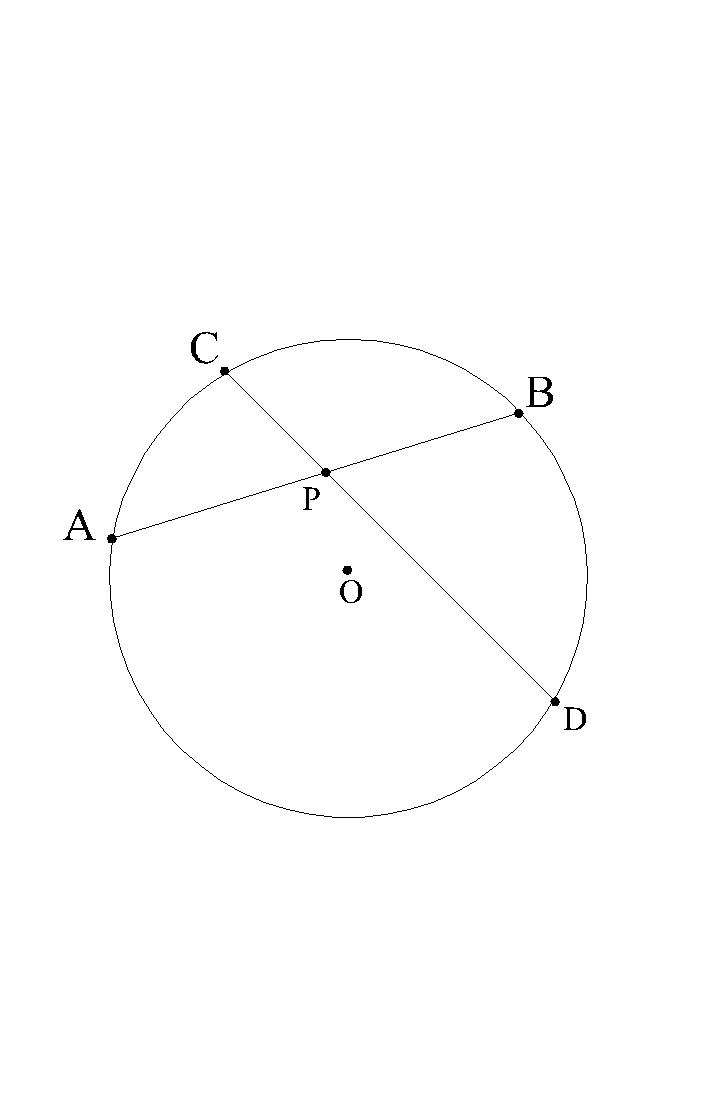
|AP|∙ |PB|= |PD|∙ |CP| i
=> |CP| =
|PD|
|PD|∙ |PD|=6∙ 8 |PD|² =48 ∙
|PD|² = 72 , |PD|>0 |PD|=6
|CP|=
∙ 6
= 4

Odp: 6
i 4
cm.

Zadanie 3. Cięciwa okręgu ma długość 10 cm. Przez jeden z końców tej cięciwy poprowadzono styczną do okręgu, w przez drugi sieczną równoległą do stycznej. Obliczyć długość promienia okręgu, jeśli wewnętrzny odcinek siecznej ma długość 12 cm.

Dane: Rozwiązanie: Szukane:

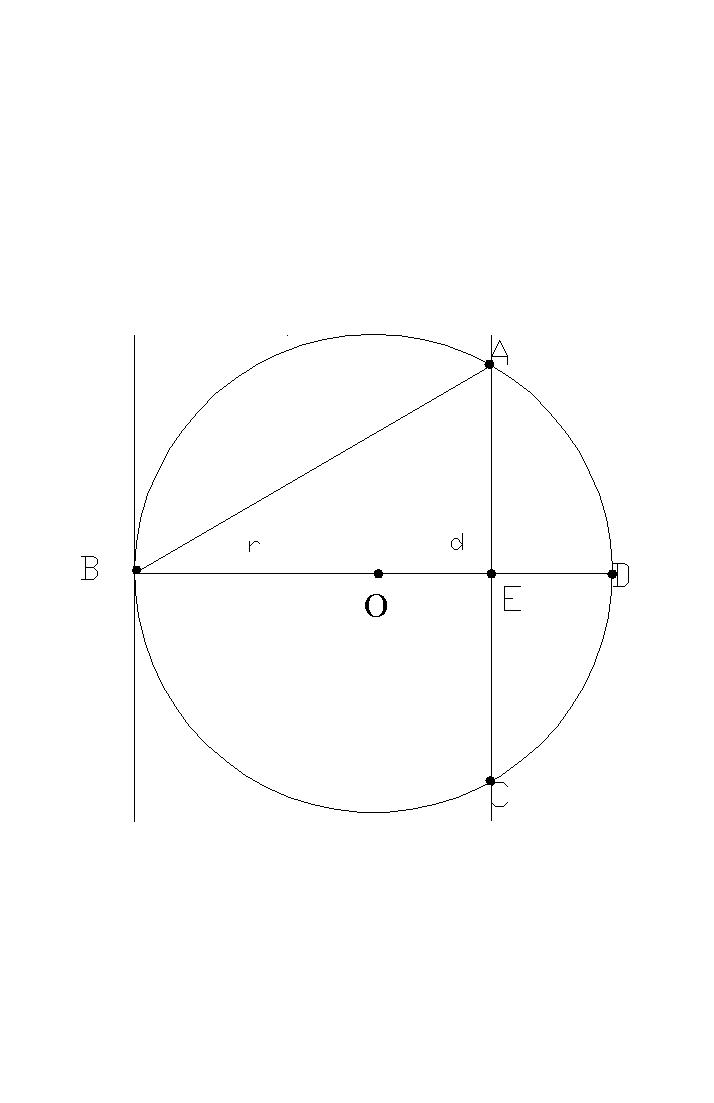
|AB|=10 cm r=|OB|=|OD| |AC|=12 cm

Niech |OE|=d Z twierdzenia o odcinkach cięciw mamy: |AE|² = (a+d)(r-d) ale |AE|=
|AC|=6 cm czyli r²-d²=36 Z trójkąta prostokątnego AEB mamy: |AE|²+|BE|² =|AB|² skąd po przestawieniu: 36+(r+d)²=100,czyli (r+d)²=64 Ponieważ r+d>0, więc r+d=8 cm Na wyznaczenie r i d należy rozwiązać układ równań r+d=8 i r²-d²=36 Skąd po wyliczeniu r=

Odp: r=6,25 cm

Zadanie 4. Punkt P jest odległy o 7 cm od środka okręgu o promieniu 11 cm. Przez punkt P poprowadzono cięciwę o długości 18 cm. Obliczyć długości odcinków, na które punkt P dzieli cięciwę.

Dane: Rozwiązanie: Szukane:

r=11 cm |AP|=x, |PB|=y |OP|=7 cm |AB|=18 cm

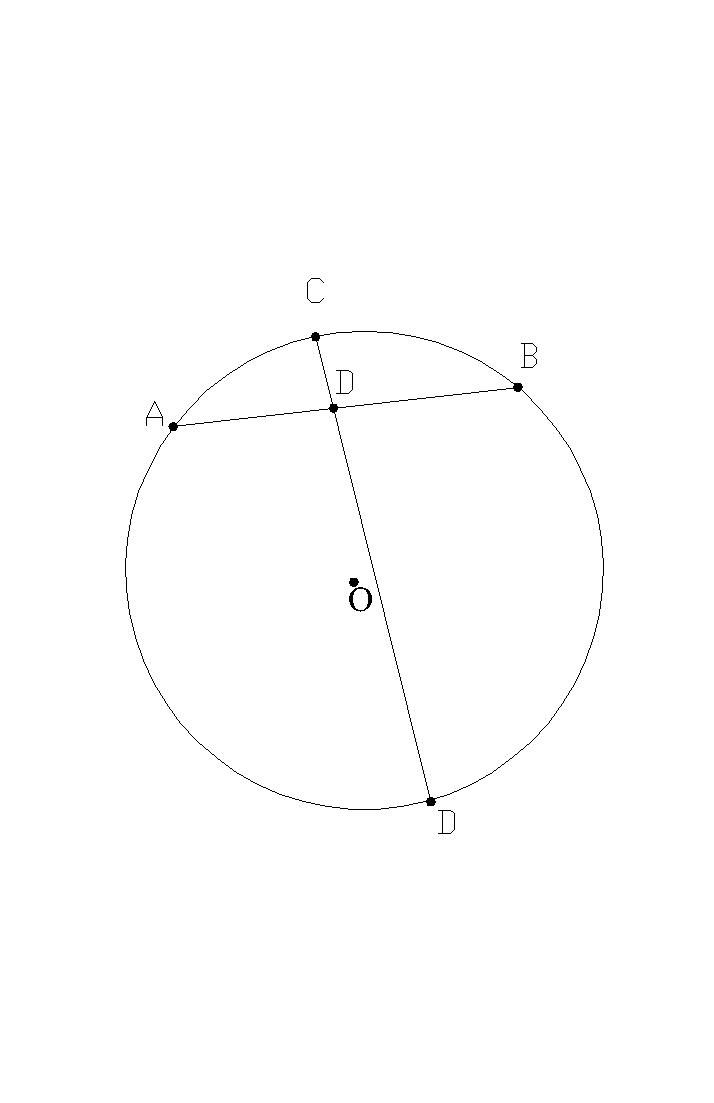
|AB|=|AP|+|PB|=x+y, czyli x+y=18 Korzystamy z twierdzenia o odcinkach przecinających się cięciw |AP|∙ |PB|=|CP|∙ |PD| Mamy: |PD|=r+|OP|=11+7=18 i |CP|=r-|OD|=11-7=4 Skąd : x∙ y= 18∙ 4=72 Rozwiązując układ równań: x+y=18 i x∙ y=72 Otrzymujemy x=12 i y=6 cm lub na odwrót.

Odp: Długości odcinków cięciwy wynoszą 12 cm i 6 cm.

Zadanie 5. Z punktu zewnętrznego okręgu poprowadzono sieczną do tego okręgu o długości 12 cm oraz styczną, której długość równa się długości wewnętrznego odcinka siecznej. Obliczyć długość stycznej.

Dane: Rozwiązanie: Szukane:

|PB|=12 cm |PC|=? |PC|=
|AB|

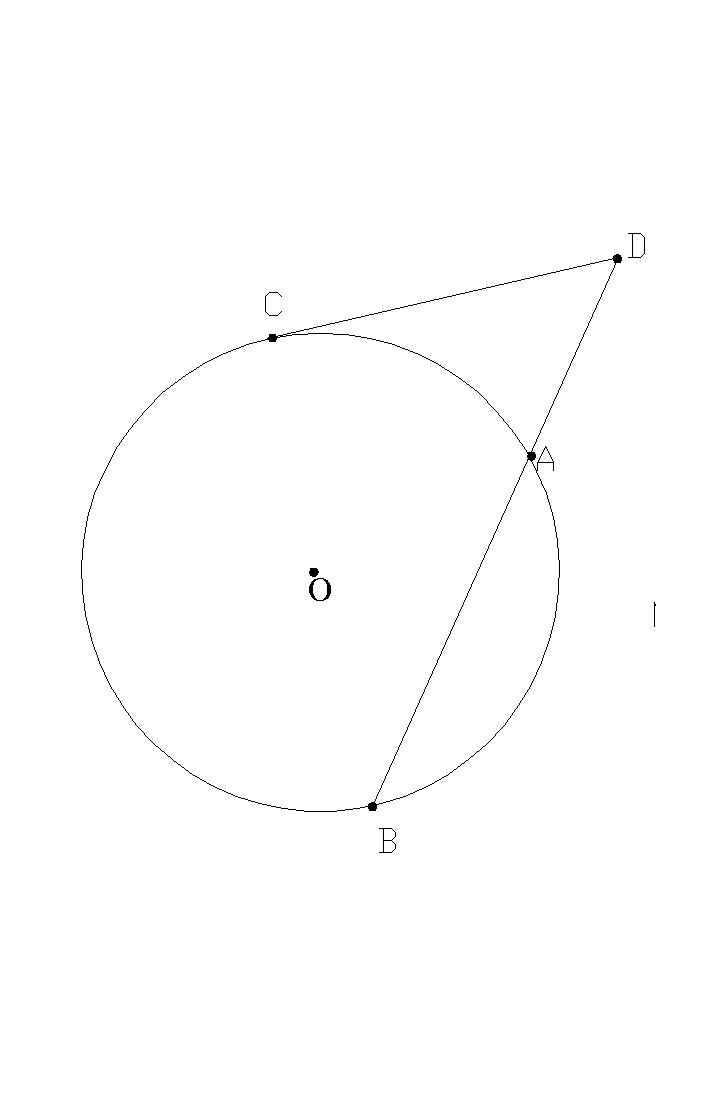
Korzystamy ze wzoru: |PC|² = |PA|∙ |PB| |PA|=|PB|-|AB|=12-
|PC| Po podstawianiu do wzoru mamy: |PC|² =(12-
|PC|)∙ 12 |PC|² =144-18|PC| |PC|²+18|PC|-144=0, |PC|=x>0 x²+18x-144=0 Po rozwiązaniu tego równania otrzymujemy: x₁=6 v x₂= -24-nie spełnia założenia

Odp: Długość stycznej wynosi 6 cm.

Zadanie 6. W okręgu o promieniu R>O poprowadzono dwie wzajemnie prostopadłe do siebie cięciwy AB i CD. Udowodnić, że |AC|² + |BD|²= 4R²

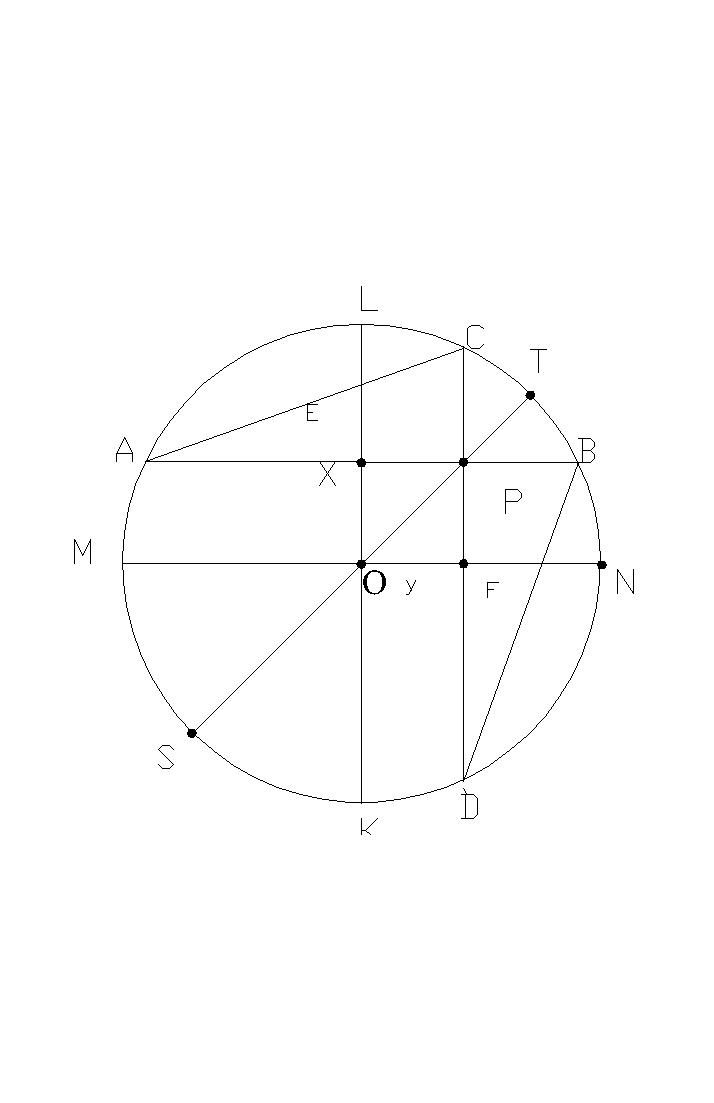
Dane: R>0 Rozwiązanie:

Korzystamy z twierdzenia i iloczynie odcinków cięciw. |AE|∙ |EB|= |KE|∙|EL| podobnie |CF|∙|FD|= |MF|∙|FN|
|AB|²=(R+x)(R-x)
|CD|²=(R+y)(R-y) |AB|²=4R²-4x² |CD|²=4R²-4y² ponadto mamy: |AP|∙|PB|=|DP| ∙ |PC| i |AP|∙ |PB|=|SP|∙ |PT| |AP|∙ |PD|=(R+
-
)= R²-( y²+x²)=R²- y²-x²

Dowód równości: L= |AC|²+|BD|² +|AP|²+|PC|²+ |DP|²+|PB|²=(|AP|+|PB|)²+=(|PC|+|DP|)² - -2|AP|∙ |PB|-2|PC|∙ |DP|= |AB|²+|CD|²-4|AP|∙|PD|=4R²-4x² +4R²-4y² - 4(R- y²-x²) =8R²-4 y²-4x²-4R²+4 y²+4x²=4R²=P

Zadanie 7. Dwa okręgi są styczne wewnętrznie w punkcie Q.Prosta przechodząca przez środek O₁ mniejszego okręgu przecina większy okrąg w punkcie A i D, a mniejszy w punktach B i C. Wyznaczyć stosunek długości promieni tych okręgów, jeżeli : |AB| : |CD| = 2:4:3

Dane: Rozwiązanie: Szukane:

|AB|:|BC|:|CD|=2:4:3
=?

Niech R i r będą promieniami tych okręgów, R>r |BC|=2r Z danej proporcji otrzymujemy: |AB|=r i |CD|=
r Z twierdzenia o odcinkach przecinających się cięciw mamy: |O₁Q|∙|O₁P|=|O₁A|∙|O₁D| skąd, wobec równośći: |O₁P|=2R-r, |O₁A|=|O₁B|+|BA|=2r i |O₁D|=|CD|+|CO₁|=
r otrzymujemy równanie:

(2R-r)r=5r² 2R-r² =5r² 2Rr=6r²/: 2r²
=3

Odp:
=3

Zadanie 8. Z punktu P leżącego na zewnątrz okręgu poprowadzono styczną i sieczną. Stosunek długości całej siecznej do długości jej odcinka wewnętrzenego jest równy 16:7. Obliczyć stosunek długości odcinka stycznej (zawartego między punktem P,a punktem styczności) do długości całej siecznej.

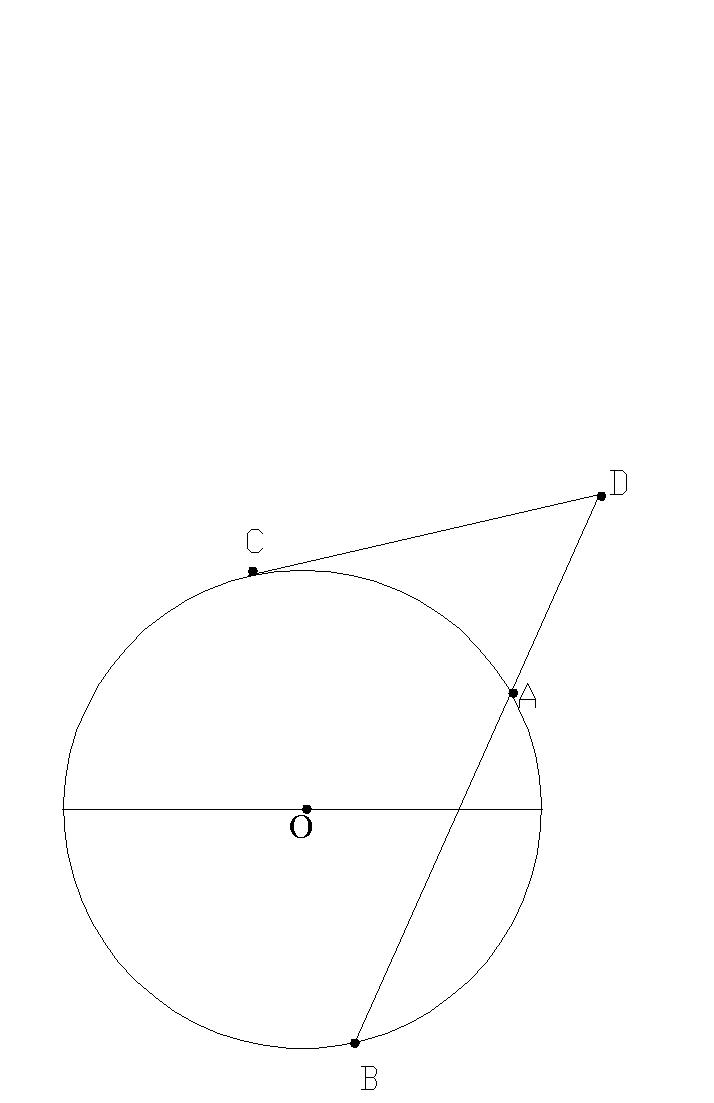
Dane: Rozwiązanie: Szukane:

|PB|:|AB|=16:7 |PC|:|PB|

Korzystamy z twierdzenia o związku pomiędzy styczną i odcinkami siecznej: |PC|² = |PA|∙ |PB| Z proporcji
=
mamy |AB|=
|PB| Następnie: |PB| = |PA|+ |AB|, skąd |PB|= |PA|+
|PB| czyli
|PB|=|PA| Po podstawieniu do wzoru |PC|² =-
|PB|∙|PB| |PC|²=
|PB|² /: |PB|²
=

=

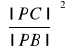
Skąd otrzymujemy
=

Odp:

Zadanie 9. Z punktu P leżącego na zewnatrz okregu poprowadzono dwie proste, z których pierwsza przecina okrąg w punktach A i B, a druga w punktach C i D.Obliczyć długości odcinków PA i PC mając dane |PA| + |DC|=20 cm oraz |PB| : |PD|=2:3

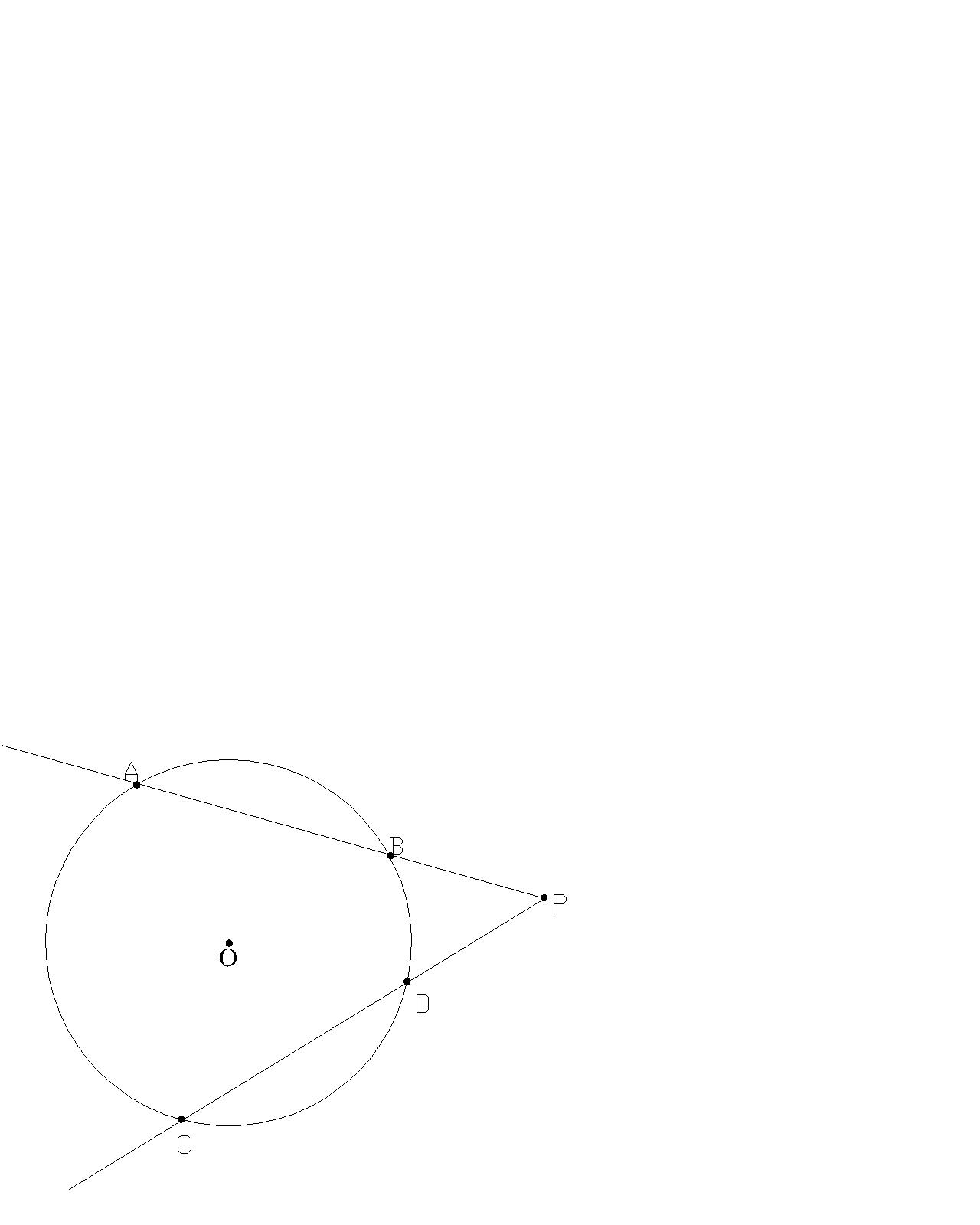
Dane: Rozwiązanie: Szukane:

|PA|+|PC|=20 cm |PA|=?
=
|PC|=?

Korzystamy z twierdzenia o ilocznie odcinków siecznych okręgu: |PA|∙ |PB|=|PD|∙|PC| × Niech |PA|= x i |PC|=y, wtedy x+y=20 Z proporcji:
=
otrzymujemy: |PB|=
|PD| co podstawiamy do ×

|PD|∙ x= |PD| y /: |PD| Zatem y=
x Następnie rozwiązujemy układ równań:
Otrzymujemy wtedy:

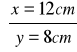
Odp: |PA|=12 cm , |PC|=8 cm.

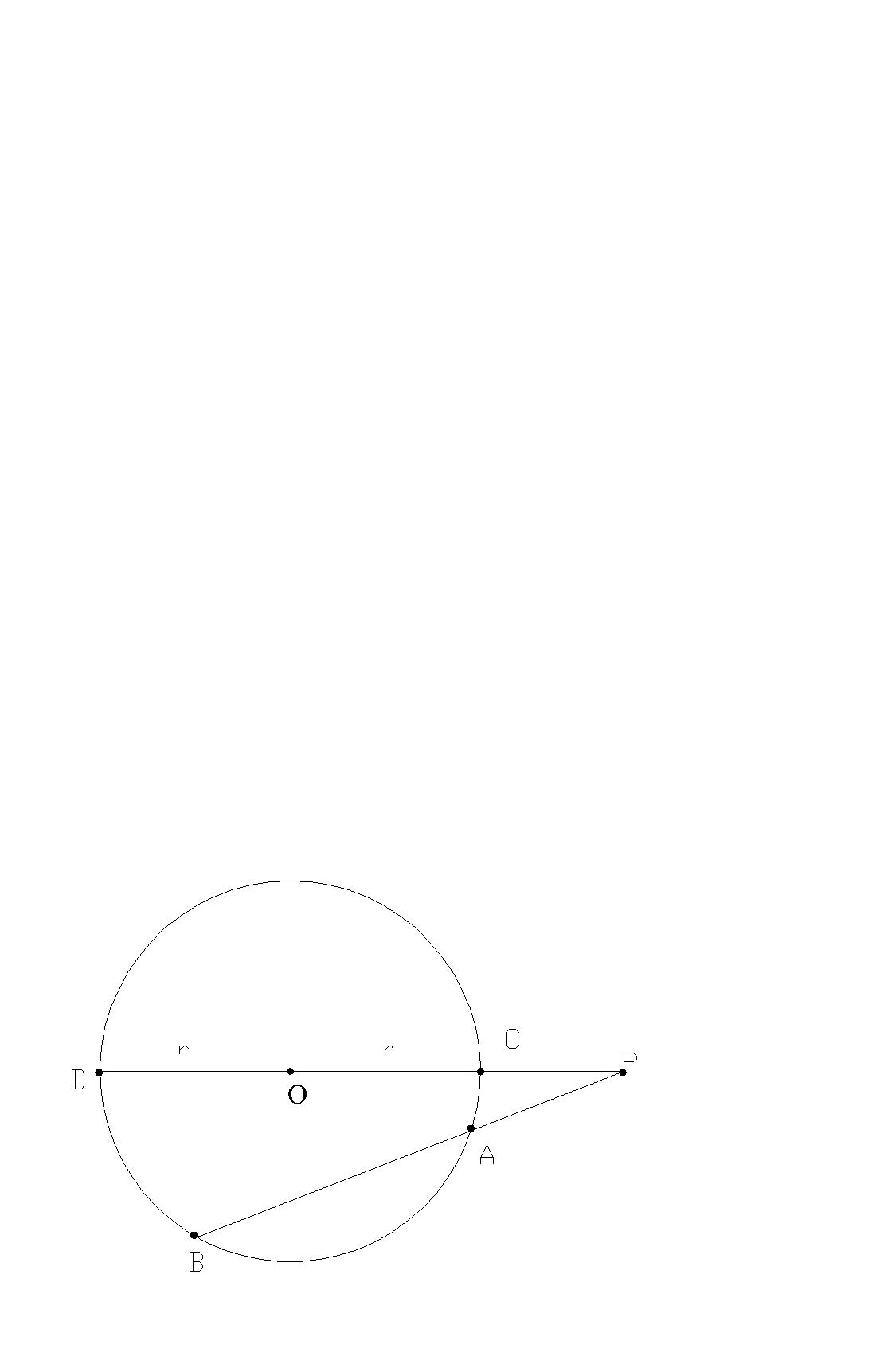
Zadanie 10. Z punktu P odległego o 11 cm od środka okręgu o promieniu 7 cm poprowadzono sieczną tak, że długość odcinków, których końcami są punkty przecięcia tej siecznej z okręgiem i punkt P, są równe. Obliczyć długości odcinka siecznej zawartego wewnątrz okręgu.

Dane: Rozwiązanie: Szukane:

|OP|=11 cm |AB|=? |OC |=r=7 cm |PA|=|AB|.

Obliczamy długość odcinka PC: |PC|=|OP|-r=11-7=4 cm Ze wzoryu na iloczyn odcinków siecznych wychodzących z jednego punktu zewnętrznego: |PD|∙ |PC|=|PB|∙|PA| po uwzględnieniu, że |PD|=2r+|CP|=2r+4=14+4=18 i |PA|=|AB| otrzymujemy : 18∙ 4=|AB|∙2|AB|. Skąd:

2|AB|² =72/: 2 |AB|²=36 i |AB| >0 |AB| =6

Odp: Długość odcinka wewnętrznego tej siecznej wynosi 6 cm.

Zadanie 11. Promień okręgu ma długość r. Z punktu M leżącego na zewnątrz poprowadzono seiczną MB przechodzącą przez środek okręgu i styczną MA, przy czym |MB|=2|MA|. Wyznaczyć odległość punktu M od środku okręgu.

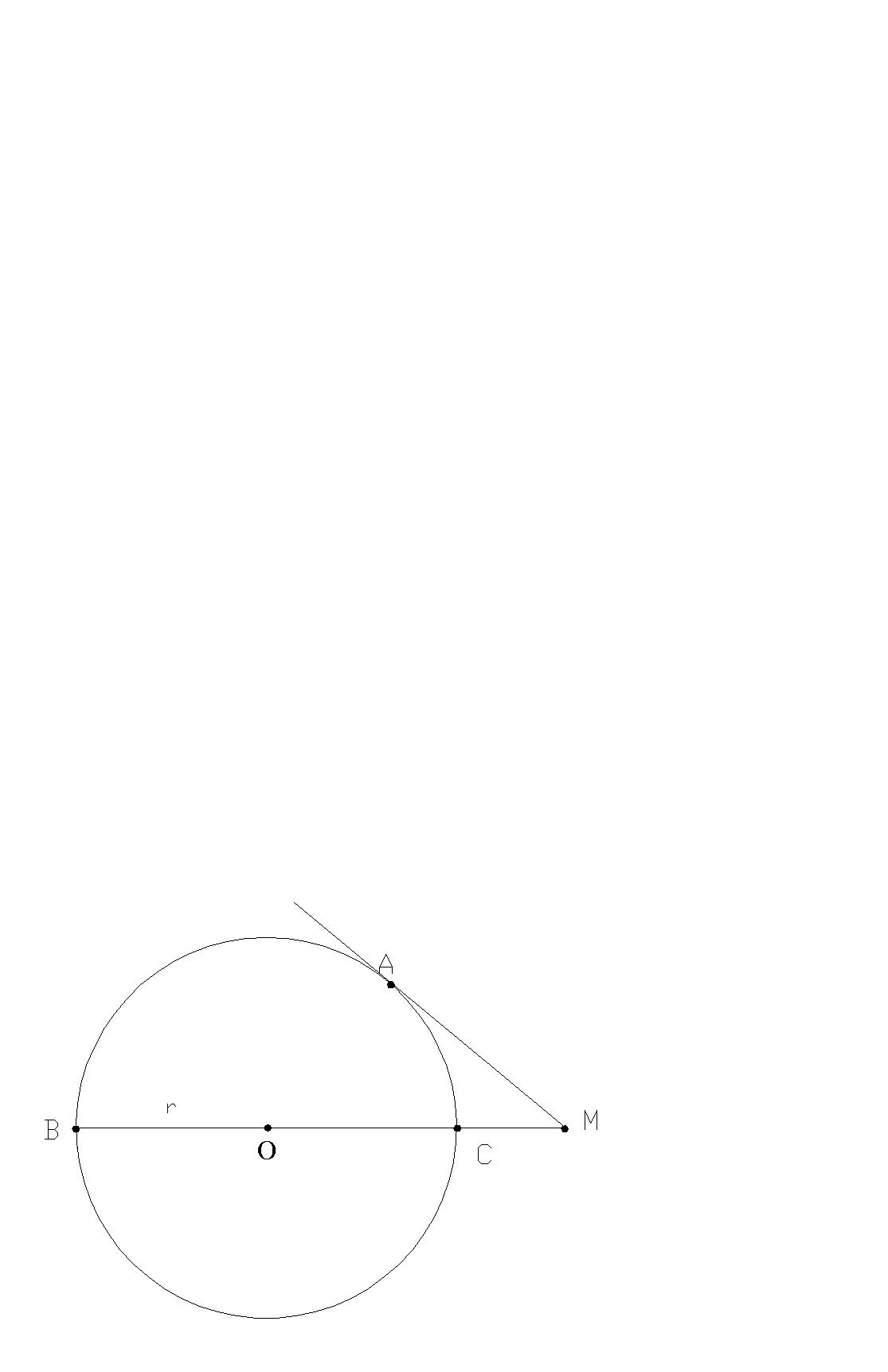
Dane: Rozwiązanie: Szukane:

a-promień okręgu |OM|=? |PB |=2|MB|

Niech |OM|=x Wtedy |BM|=x+r i |CM|=x-r oraz na podstawie założenia |MA|= Na podstawie wzoru |MA|²=|BM|∙|CM| otrzymujemy :
(x+r) ²=(x+r)(x-r), skąd po uproszczeniu przez x+r otrzymujemy równanie:

(x+r) =x-r z którego wyznaczamy x=
r

Odp: |MO|=
r

Zadanie 12.Z punktu leżącego na okręgu poprowadzono dwie cięciwy o długościach 10 cm i 12 cm. Oblicz promień tego okręgu,jeżeli odległość środka mniejszej cięciwy od większej cięciwy jest równa 4 cm.

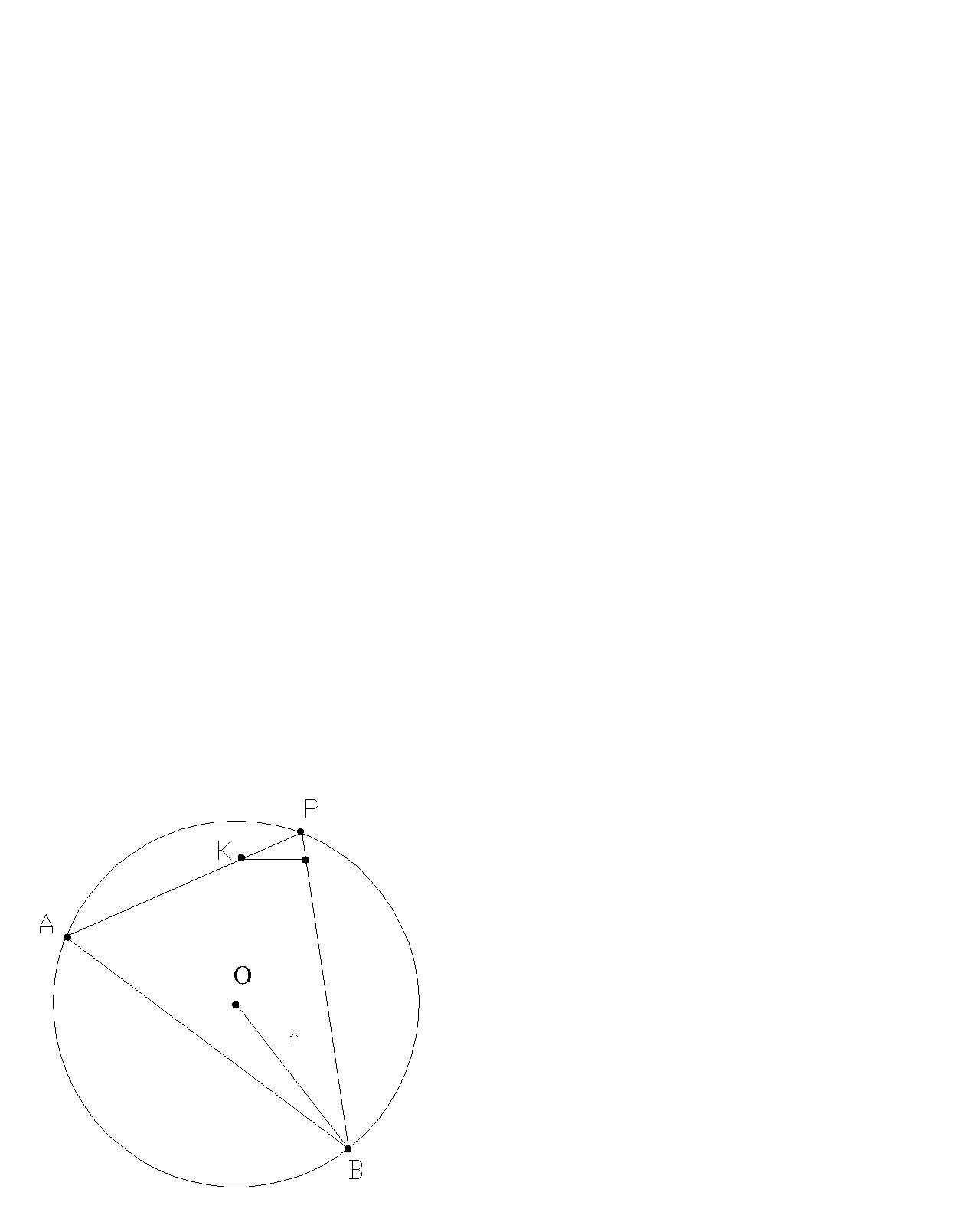
Dane: Rozwiązanie: Szukane:

|PA|=10 cm promień r-? |PB |=12 cm |KL|=4 cm

Niech |OB|=r |
APB|= α Δ PLK jest prostokątny => sinα = =
, bo |PK|=
|AD|=5 jeżeli sinα =
, to z „jedynki trygonometrycznej” cosα=
Stosując do ΔAPB tw.cosinusów obliczamy |AB|. Mianowicie: |AB|²=|AD|² + |PB|² - 2|AD|∙|PB|∙cosα |AB|²=100+144-2∙10∙ 12∙
=244-144=100 skąd |AB|=10 cm Ze wzoru sinusów:
= 2 r

Obliczamy r=
=
=
= 10
=
=
=6,25 cm

Odp: a=6,25

---