Politechnika Lubelska	Laboratorium Elektrotechniki
w Lublinie	Ćwiczenie nr 5 a,c
Klukowski Tadeusz Kisiel Krzysztof Kowalczyk Dariusz		Semestr IV	Grupa: 4.1	Rok akademicki: 1997/98
Temat ćwiczenia: Modelowanie pól płaskich na papierze elektroprzewodzącym			Data wykonania: 98.03.02	Ocena:

Wykonanie ćwiczenia.

1).Część 5a.

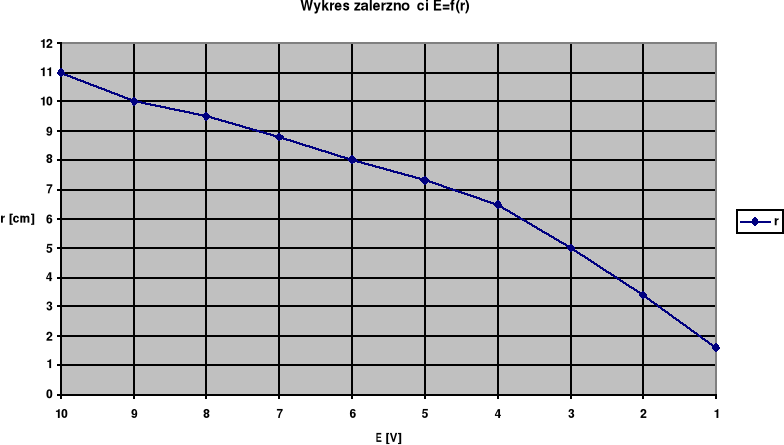
a). Badanie rozkładu natężenia pola.

b). Układ do pomiaru rozkładu natężenia pola dla kabla koncentrycznego.

c).Układ do pomiaru metodą zadania odwrotnego.

Tabela dla układu kabla koncentrycznego

V	[V]		10		9		8		7		6		5		4		3		2		1
R	cm	11		10		9,5		8,8		8		7,3		6,5		5		3,4		1,6

2. Część 5 c

W tej części dokonujemy pomiarów tych samych układów lecz przy pomocy programu komputerowego. Uzyskane wyniki porównujemy z wynikami wyznaczonymi analitycznie.

Rys.1. Rozkład linii ekwipotencjalnych dla kabla koncentrycznego w polu elektrostatycznym.

Rys.2. Mapa pola elektrycznego dla walców współosiowych .

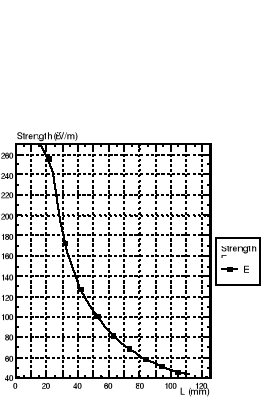
Rys.3. Potencjał V(r) i natężenie pola elektrycznego E(r) wzdłuż promienia układu walców

Współosiowych.

Rys.4. Wykres rozkładu linii ekwipotencjalnych w przewodzie wyznaczony metodą zadania odwrotnego.

Rys.5. Wykres rozkładu linii ekwipotencjalnych i obraz wektorów gęstości prądu w przewodzie o zmiennym

przekroju.

Obliczenia Przeprowadzone przy pomoc programu komputerowego.

1) Sprawdzenie prawa Gaussa.

2a) Sprawdzenie pierwszego prawa Kirchhoffa

3) Sprawdzenie drugiego prawa Kirchhoffa

OBLICZENIA:

1. pole układu o symetrii cylindrycznej

−natężenie pola elektrycznego dla kabla koncentrycznego o długości l=1m.

E=I/(2πγl∗r) γ=1/(R∗h)

γ=1/(1190Ω∗1.32E-04m.)=6.34 [1/Ωm.]

I=26mA r=0.11m. l=1m.

E=5.93E-03 [V/m.]

− rezystancja przejścia

Rp=U/I

RP=10V/0.026A=384.62Ω

− pojemność kondensatora elementarnego C′ oraz pojemność całego układu C

C′=ε∗a∗h/d

C=C′∗n/(m.+1)

ε−przenikalność elektryczna próżni

h−1m

d−odległość między okładkami kondensatora elementarnego C′

a− wysokość okładek C′

m−liczba powierzchni ekwipotencjalnych z wyłączeniem powierzchni okładzin

m.+1−liczba szeregowo połączonych kondensatorów C′

n−liczba łańcuchów połączonych równolegle

n=9 m.=7 a=1.4E-02m. h=1m. d=3.4E-02m. ε=8.85E-12 [F/m.]

C′=3.42E-11 F

C=2.73E-11F

C=2π∗ε∗h/[ln(r2/r1)] r1=0.015m. r2=0.11m.

C= 2.8E-11 F

2. pole w przewodniku o zmiennym przekroju

−rezystancja przejścia układu uzyskana doświadczalnie ,

Rp=ρ∗(l1/S1+l2/S2+l3/S3)

ρ=R∗h=1190Ω∗1.32E-04m.=0.15708

l1 =0.12m. S1=1.584E-05m² l2=0.12m. S2=1.584E-05m² l3=0.05m. S3=2.64E-06

Rp=3522.4Ω

−rezystancja przejścia układu uzyskana analitycznie ,

Rp=U/I

U−napięcie zasilania układu ,

I−prąd w układzie ,

U=10V I=2.6mA

Rp=10V/2.6mA=3846.2Ω

Wnioski

Na podstawie otrzymanych wartości można zauważyć , że znacznie prostszą metodą od metody rozwiązywania równań Laplace′a jest metoda graficzna . Wymaga ona znacznie mniejszego nakładu czasu, środków i wysiłku : wystarcza woltomierz cyfrowy oraz papier półprzewodzący i można analizować bardzo skomplikowane przypadki , których obliczenie zajęło by bardzo dużo czasu , gdy metodą graficzną wykreślenie rozkładu pola nie stwarza większego problemu .

Przy bardziej skomplikowanych przypadkach ta metoda jednak nie wystarcza . Wtedy najlepszym rozwiązaniem jest wykorzystanie programu komputerowego .Umożliwia on złożenie badanego

układu i nadanie różnym elementom określonych parametrów .

Wyniki uzyskane przy pomocy komputera charakteryzuje duża dokładność. , przejrzystość i szybkość ( pod warunkiem wcześniejszego dokładnego zapoznania się z programem) , możemy policzyć dowolne parametry na wybranym polu badanego układu. Na pewno metoda komputerowej analizy rozkładu pola jest bardzo wygodna .

7

(



Q

D

ds





Q

2

10

1

416

10





.

*

1

2

Q

1

13

2

515

10







.

Ids





1

1)

Ids





0

382

.

2

2)

Ids





2022222222

2.28

.

Edl





0

1

U



0

025457 VV

.

---