Analiza współzależności badanych cech
1. Test chi-kwadrat
Dla sprawdzenia przypuszczenia o współzależności między badanymi cechami wykorzystuje się nieparametryczny test niezależności chi-kwadrat (χ2). Test ten stosowany jest w badaniach, w których przynajmniej jedna z badanych cech ma charakter jakościowy. Przed przystąpieniem do realizacji poszczególnych etapów analizy współzależności dwóch cech niezbędne jest skonstruowanie tablicy dwudzielnej cech: X i Y.
|
yj xi |
y1 |
Poziomy Y2 |
cechy Y … |
yk |
j |
|
x1 |
n11 |
n12 |
... |
n1k |
n1.. |
Poziomy |
x2 |
n21 |
n22 |
... |
n2k |
n2.. |
cechy |
... |
... |
... |
... |
... |
... |
X |
... |
... |
... |
... |
... |
... |
|
xl |
nl1 |
nl2 |
... |
nlk |
nl.. |
|
i |
n..1 |
n..2 |
... |
n.k |
n |
Krok 10 Przyjęcie hipotez
H0 : cechy X i Y są niezależne. Hipoteza zerowa H0 ma miejsce wówczas, gdy mniemamy, że pomiędzy estymatorem i parametrem lub rozkładem teoretycznym i empirycznym nie ma statystycznie istotnej różnicy.
H1 : cechy X i Y nie są niezależne. Hipoteza alternatywna H1 dopuszcza istnienie różnic pomiędzy estymatorami (statystykami) i parametrami, jak też pomiędzy rozkładami z prób i rozkładami teoretycznymi.
Krok 20 Statystyka testowa:
gdzie są to tak zwane liczebności teoretyczne.
ni - liczba elementów próby odpowiadających poziomowi xi cechy X,
nj - liczba elementów próby odpowiadających poziomowi yj cechy Y,
nij - liczba elementów próby odpowiadających poziomowi xi cechy X
i poziomowi yj cechy Y,
n - suma elementów próby odpowiadających poziomowi xi cechy X i poziomowi yj
cechy Y,
k - liczba kolumn,
l - liczba wierszy
Krok 30 Przyjęcie poziomu istotności
Za pomocą współczynnika ufności określa się prawdopodobieństwo, że podjęta decyzja jest decyzją słuszną. Jeżeli wartości przyjęte w hipotezie w znaczny sposób odbiegają od wyniku statystyk uzyskanych na podstawie próby, to z dużą pewnością hipotezę taką możemy odrzucić. Wówczas współczynnik ufności jest bardzo niski. Natomiast, jeżeli hipoteza jest zbliżona do wyników próby, to z coraz mniejszą pewnością można stwierdzić, że hipoteza jest fałszywa. W takim przypadku współczynnik ufności przyjmuje wartość bliską jedności.
W analizie przyjęto współczynnik ufności 1 - = 0,90, oznacza to, że średnio w 10-ciu przypadkach na 100 popełniono błąd. Poziom istotności oznacza prawdopodobieństwo popełnienia błędu. Poziom istotności: 1 - = 0,90 ⇒ = 0,1
Krok 40
Wyznaczenie obszaru krytycznego:
![]()
wartość statystyki przy określonym poziomie istotności - i liczbie stopni swobody - v.
Aby odczytać wyżej wymienioną wartość z tablic należy obliczyć liczbę stopni swobody, korzystając z następującego wzoru:
v = (k - 1) (l - 1)
k - liczba kolumn,
l - liczba wierszy.
Obszar krytyczny wyznacza się w celu sprawdzenia czy konkretna realizacja χ2 statystyki testowej należy do obszaru.
Jeżeli po obliczeniu, χ2 nie należy do obszaru krytycznego to przyjmuje się hipotezę zerową H0 za prawdziwą. Natomiast jeżeli χ2 należy do obszaru krytycznego odrzuca się wtedy hipotezę zerową na korzyść hipotezy alternatywnej H1.
Krok 50 Obliczenie konkretnej realizacji χ2 statystyki testowej.
Krok 60 Podjęcie decyzji:
jeżeli χ2 ∈ K ⇒ odrzucamy hipotezę H0 na korzyść hipotezy H1,
jeżeli χ2 ∉ K ⇒ nie ma podstaw do odrzucenia hipotezy H0.
Po odrzuceniu H0 na korzyść H1, czyli przyjęciu, że cechy X i Y są od siebie zależne, należy obliczyć wskaźnik kontyngencji:
χ2 - konkretna realizacja statystyki - obliczona ze wzoru 20
n - suma elementów próby odpowiadających poziomowi xi cechy X i poziomowi yj
cechy Y,
k - liczba kolumn, l - liczba wierszy.
Wartość C wskazuje, jak silna jest zależność badanych cech.
4.1.1 Zależność pomiędzy poglądem na temat kredytu samochodowego a wiekiem
Celem przeprowadzonej analizy było zbadanie postawy respondentów wobec kredytu samochodowego w zależności od wieku. Do oceny współzależności badanych cech jakościowych zastosowano wyżej opisany test chi-kwadrat, opierając się o jego kolejne etapy.
Cecha X: postawa wobec kredytu samochodowego.
Cecha Y: wiek respondentów.
|
yj |
|
Poziom |
cechy Y |
|
j |
P |
xi |
< 25 |
26 - 40 |
41 - 60 |
>60 |
|
o z |
Tak |
2 |
13 |
5 |
4 |
24 |
i o |
Raczej tak |
1 |
9 |
20 |
10 |
40 |
m
|
Trudno powiedzieć |
0 |
10 |
13 |
17 |
40 |
ce- chy |
Raczej nie |
1 |
14 |
18 |
28 |
61 |
X |
Nie |
4 |
8 |
16 |
7 |
35 |
|
i |
8 |
54 |
72 |
66 |
200 |
Tab. 4.2.
10
H0: cechy X i Y są niezależne.
Postawa wobec kredytu samochodowego jest niezależna od wieku respondentów.
H1: cechy X i Y nie są niezależne.
Postawa wobec kredytu samochodowego nie jest niezależna od wieku respondentów.
20
Statystyka testowa:
30
Przyjęcie poziomu istotności: 1 - = 0,90 ⇒ = 0,1
40
Wyznaczenie obszaru krytycznego:
Obliczenie liczby stopni swobody:
v = (k - 1) (l - 1) k = 4 l = 5 v = (4 - 1) (5 - 1) = 12
50
Obliczenie konkretnej realizacji χ2 statystyki testowej. (Wykorzystano wzór 20).
Ze względu na zbyt dużą liczbę danych, w powyższym obliczeniu zobrazowano jedynie sposób liczenia. Uznano, że przedstawienie wszystkich rachunków jest zbyteczne, gdyż i tak do dalszych etapów wykorzystywany jest tylko wynik.
Obliczona wartość χ2 jest większa od wartości odczytanej z tablicy (30>18,55), wobec tego należy do obszaru krytycznego.
Decyzja:
Decyzja:
χ2 ∈ K ⇒ odrzucamy H0 na korzyść H1.
Wniosek:
Postawa wobec kredytu jest zależna od wykształcenia respondentów.
Ponieważ χ2 ∈ K przystąpiono do obliczenia wskaźnika kontyngencji:
Wskaźnik kontyngencji wynosi 0,257; wskazuje to na słabą zależność między cechami. Można stąd wysnuć wniosek, że negatywne bądź pozytywne podejście do kredytu nie jest bardzo mocno związane z posiadanym wykształceniem.
Wniosek:
Pogląd na temat kredytu samochodowego jest zależny od wieku respondentów. Na tym poziomie istotności między omawianymi cechami istnieje powiązanie choć nie jest ono bardzo silne.
4.1.2 Zależność preferowanych atrybutów samochodowych od płci badanych
Celem analizy było zbadanie, czy wybór atrybutów samochodowych zależy od płci badanych. Jako instrument pomiaru zastosowano test chi-kwadrat oceny współzależności cech X i Y.
Cecha X: atrybuty samochodowe.
Cecha Y: płeć respondentów.
|
yj |
Poziomy y1 kobieta |
cechy Y y2 mężczyzna |
j |
|
xi |
|
|
|
|
x1 Wygląd samochodu i jego elegancja |
83 |
80 |
163 |
|
x2 Wierność firmie |
18 |
21 |
39 |
|
x3 Korzystna cena |
73 |
63 |
136 |
|
x4 Komfort jazdy |
75 |
71 |
146 |
|
x5 Osiągi trakcyjne |
40 |
53 |
93 |
P |
x6 Niski poziom hałasu |
37 |
44 |
81 |
o |
x7 Obszerne wnętrze |
51 |
63 |
114 |
z |
x8 Bezpieczeństwo |
85 |
74 |
159 |
i |
x9 Pojemność bagażnika |
26 |
18 |
44 |
o |
x10 Pojemność baku |
12 |
15 |
27 |
m |
x11 Instalacja gazowa |
1 |
12 |
13 |
y |
x12 Wtrysk paliwa |
9 |
35 |
44 |
|
x13 Felgi aluminiowe |
10 |
23 |
33 |
c |
x14 Wspomaganie kierownicy |
62 |
64 |
126 |
e |
x15 ABS |
54 |
64 |
118 |
c |
x16 Automatyczna skrzynia biegów |
19 |
10 |
29 |
h |
x17 Poduszka powietrzna dla kierowcy |
58 |
61 |
119 |
y |
x18 Poduszka powietrzna dla pasażera |
43 |
42 |
85 |
|
x19 Poduszki powietrzne boczne |
24 |
17 |
41 |
X |
x20 Fabryczne zabezpieczenia przeciwkradzieżowe |
37 |
33 |
70 |
|
x21 Klimatyzacja |
46 |
47 |
93 |
|
x22 Szyberdach |
12 |
15 |
27 |
|
x23 Elektrycznie opuszczane szyby |
19 |
24 |
43 |
|
x24 Elektrycznie regulowane lusterka |
9 |
9 |
18 |
|
x25 Centralny zamek |
51 |
61 |
112 |
|
x26 Komputer pokładowy |
6 |
21 |
27 |
|
i |
960 |
1040 |
2000 |
Tab. 4.3.
10
H0: cechy X i Y są niezależne.
Preferowane atrybuty samochodów są niezależne od płci respondentów.
H1: cechy X i Y nie są niezależne.
Preferowane atrybuty samochodów nie są niezależne od płci respondentów.
20
Statystyka testowa:
30
Przyjęcie poziomu istotności: 1 - = 0,90 ⇒ = 0,1
40
Wyznaczenie obszaru krytycznego:
Obliczenie liczby stopni swobody:
v = (k - 1) (l - 1) k = 2 l = 26 v = (2 - 1) (26 - 1) = 25
50
Obliczenie konkretnej realizacji χ2 statystyki testowej. (Wykorzystano wzór 20).
Ze względu na zbyt dużą liczbę danych, w powyższym obliczeniu zobrazowano jedynie sposób liczenia. Uznano, że przedstawienie wszystkich rachunków jest zbyteczne, gdyż i tak do dalszych etapów wykorzystywany jest tylko wynik.
60
Obliczona wartość χ2 jest większa od wartości odczytanej z tablicy (49,37>34,38), wobec tego należy do obszaru krytycznego.
Decyzja:
χ2 ∈ K ⇒ odrzucamy H0 na korzyść H1.
Wniosek:
Gama preferowanych atrybutów jest zależna od płci respondentów.
Ponieważ χ2 ∈ K przystąpiono do obliczenia wskaźnika kontyngencji:
Wskaźnik kontyngencji wynosi 0,878; wskazuje to na silną zależność między cechami. Można stąd wysnuć wniosek, że preferencje kobiet w zakresie atrybutów samochodowych znacznie się różnią od upodobań mężczyzn.
4.1.3 Zależność preferowanych atrybutów samochodowych od
wieku respondentów
Celem analizy było zbadanie, czy wybór atrybutów samochodowych zależy od wieku badanych. Jako instrument pomiaru zastosowano test chi-kwadrat oceny współzależności cech X i Y.
Cecha X: atrybuty samochodowe.
Cecha Y: wiek respondentów.
|
yj |
y1 wiek <25 |
Poziomy y2 26-40 |
Cechy Y y3 41-60 |
y4 >60 |
j |
|
xi |
|
|
|
|
|
|
x1 Wygląd i elegancja samochodu |
56 |
58 |
45 |
4 |
163 |
|
x2 Wierność firmie |
10 |
15 |
10 |
4 |
39 |
|
x3 Korzystna cena |
49 |
47 |
36 |
4 |
136 |
|
x4 Komfort jazdy |
46 |
56 |
38 |
6 |
146 |
|
x5 Osiągi trakcyjne |
33 |
28 |
26 |
6 |
93 |
P |
x6 Niski poziom hałasu |
33 |
26 |
20 |
2 |
81 |
o |
x7 Obszerne wnętrze |
28 |
44 |
39 |
3 |
114 |
z |
x8 Bezpieczeństwo |
51 |
59 |
41 |
8 |
159 |
i |
x9 Pojemność bagażnika |
12 |
20 |
12 |
0 |
44 |
o |
x10 Pojemność baku |
5 |
14 |
8 |
0 |
27 |
m |
x11 Instalacja gazowa |
3 |
5 |
5 |
0 |
13 |
y |
x12 Wtrysk paliwa |
8 |
19 |
15 |
2 |
44 |
|
x13 Felgi aluminiowe |
12 |
13 |
6 |
2 |
33 |
c |
x14 Wspomaganie kierownicy |
44 |
41 |
35 |
6 |
126 |
e |
x15 ABS |
43 |
38 |
30 |
7 |
118 |
c |
x16 Automatyczna skrzynia biegów |
5 |
18 |
6 |
0 |
29 |
h |
x17 Poduszka powietrzna kierowcy |
42 |
40 |
31 |
6 |
119 |
y |
x18 Poduszka powietrzna pasażera |
28 |
31 |
22 |
4 |
85 |
|
x19 Poduszki powietrzne boczne |
13 |
11 |
15 |
2 |
41 |
X |
x20 Fabryczne zabezpieczenia przeciwkradzieżowe |
20 |
29 |
19 |
2 |
70 |
|
x21 Klimatyzacja |
31 |
30 |
30 |
2 |
93 |
|
x22 Szyberdach |
11 |
11 |
4 |
1 |
27 |
|
x23 Elektrycznie opuszczane szyby |
21 |
13 |
8 |
1 |
43 |
|
x24 Elektrycznie regulowane lusterka |
5 |
9 |
4 |
0 |
18 |
|
x25 Centralny zamek |
40 |
38 |
28 |
6 |
112 |
|
x26 Komputer pokładowy |
11 |
7 |
7 |
2 |
27 |
|
i |
660 |
720 |
540 |
80 |
2000 |
Tab. 4.4.
10
H0: cechy X i Y są niezależne.
Preferowane atrybuty samochodów są niezależne od wieku respondentów.
H1: cechy X i Y nie są niezależne.
Preferowane atrybuty samochodów nie są niezależne od wieku respondentów.
20
Statystyka testowa:
30
Przyjęcie poziomu istotności: 1 - = 0,90 ⇒ = 0,1
40
Wyznaczenie obszaru krytycznego:
Obliczenie liczby stopni swobody:
v = (k - 1) (l - 1) k = 4 l = 26 v = (4 - 1) (26 - 1) = 75
50
Obliczenie konkretnej realizacji χ2 statystyki testowej. (Wykorzystano wzór 20).
Ze względu na zbyt dużą liczbę danych, w powyższym obliczeniu zobrazowano jedynie sposób liczenia. Uznano, że przedstawienie wszystkich rachunków jest zbyteczne, gdyż i tak do dalszych etapów wykorzystywany jest tylko wynik.
60
Obliczona wartość χ2 jest mniejsza od wartości odczytanej z tablicy (64,51<85,53), wobec tego nie należy do obszaru krytycznego.
Decyzja:
χ2 ∉ K ⇒ nie ma podstaw do odrzucenia H0.
Wniosek:
Pogląd na temat preferowanych atrybutów samochodowych nie jest zależny od wieku respondentów. Na tym poziomie istotności różnica między omawianymi cechami jest nieistotna i spowodowana losowym charakterem próby.
4.2 Analiza wariancji
Analiza wariancji pomaga udzielić odpowiedzi na pytanie o wpływ zmiennej eksperymentalnej na zmienne zależne. Metoda ta jest techniką statystyczną pozwalającą badaczowi na określenie problemu, czy różnice między średnimi z prób są większe niż oczekiwane, spowodowane błędem próby. Analiza znalazła zastosowanie przede wszystkim do testowania eksperymentów przeprowadzonych za pomocą kwadratu łacińskiego, modelu czynnikowego lub eksperymentu całkowicie losowego.
Aby przeprowadzić badanie tą metoda analizy należy wykonać następujące kroki23:
10
Skonstruować tabelę zawierającą bezwzględne wielkości badanych zmiennych otrzymane z pomiarów. Wzór tabeli prezentuje rys 4.3.
|
yj xi |
y1 |
Poziomy Y2 |
cechy Y … |
yk |
j |
|
|
x1 |
n11 |
n12 |
... |
n1k |
n1.. |
|
Poziomy |
x2 |
n21 |
n22 |
... |
n2k |
n2.. |
|
cechy |
... |
... |
... |
... |
... |
... |
… |
X |
... |
... |
... |
... |
... |
... |
… |
|
xl |
nl1 |
nl2 |
... |
nlk |
nl.. |
|
|
i |
n..1 |
n..2 |
... |
n.k |
n |
|
|
|
|
|
… |
|
|
|
Rys. 4.5
20
Następnie na podstawie otrzymanych danych w tabeli formułowane są pytania, czy wynikające różnice są rezultatem rzeczywistych preferencji ankietowanych, czy też wynikają z różnic w preferencjach określonych drugą zmienną. Innym możliwym wyjaśnieniem może być założenie, że ze względu na próby losowe różnice mogą być spowodowane błędem wynikającym z doboru próby. Na podstawie tych pytań konstruowane są dwie hipotezy zerowe.
30
Kolejnym proceduralnym krokiem, jaki należy zrobić w obliczeniach, jest budowa tablicy roboczej umożliwiającej wyodrębnienie rodzajów informacji, jakie należy zebrać do obliczeń. Ponadto tablica ta zawiera instrukcje obliczenia wskaźnika F. Wskaźnik F służy do analizy wartości krytycznej rozkładu F dla stopnia swobody liczonego dla danego licznika i mianownika przy określonym poziomie istotności ![]()
. Obliczona wartość wskaźnika jest podstawą do przyjęcia którejś z postawionych hipotez za prawdziwą.
Rodzaj zależności |
Suma kwadratów |
Stopnie swobody |
Średni kwadrat (SK) |
Wskaźnik F |
Zależność między rozkładem pierwszej zmiennej |
Suma kwadratów zmiennych eksperymentalnych (SK1); suma kwadratów w wierszach |
l - 1 (liczba wierszy minus 1) |
|
|
Zależność między rozkładem drugiej zmiennej |
Suma kwadratów (SK2); suma kwadratów w kolumnach |
k - 1 (liczba kolumn minus 1) |
|
|
Błąd średniego kwadratu |
Cząstkowe sumy kwadratów (CSK) |
(k-1)(l-1) |
|
|
Ogólna suma kwadratów |
OSK |
kl-1 |
|
|
Tab. 4.6
40
Następnie można przystąpić do obliczania wartości liczbowych określonych w powyższej tablicy na podstawie empirycznych danych zawartych w tablicy zmiennych( tab 4.1). Należy ustalić wartość dwóch wskaźników F dla poszczególnych zmiennych. W tym celu korzystamy z następujących wzorów:
1.
![]()
gdzie:
SK1 - suma kwadratów pierwszej zmiennej eksperymentalnej,
![]()
- średnia elementów próby odpowiadająca poszczególnym wierszom,
![]()
- średnia ogólna liczona z wzoru:
![]()
gdzie: n - suma elementów próby odpowiadających poziomowi zmiennej xi i poziomowi zmiennej yj
l - liczba wierszy,
k - liczba kolumn.
2.
![]()
gdzie:
SK2 - suma kwadratów drugiej zmiennej eksperymentalnej,
![]()
- średnia elementów próby odpowiadająca poszczególnym kolumnom,
![]()
- średnia ogólna
l - liczba wierszy,
k - liczba kolumn
3.
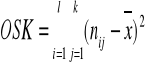
gdzie:
OSK -ogólna suma kwadratów,
![]()
- liczba elementów próby odpowiadających poziomowi zmiennej xi i poziomowi zmiennej yj
![]()
- średnia ogólna liczona z wzoru:
l - liczba wierszy,
k - liczba kolumn
4.
![]()
gdzie:
CSK - cząstkowe sumy kwadratów
OSK - ogólna suma kwadratów,
SK1 - suma kwadratów pierwszej zmiennej eksperymentalnej,
SK2 - suma kwadratów drugiej zmiennej eksperymentalnej.
50
Po obliczeniu wskaźników F dla zmiennej eksperymentalnej i drugiej zmiennej należy porównać otrzymane wartości w wartością krytyczną rozkładu F. Wartość ta zależy od stopnia swobody zarówno w liczniku (n), jak i w mianowniku (m) wskaźnika F i od przyjętego poziomu ufności. Wzory do ustalenia wartości liczebników i mianownika są następujące:
n1 = (l - 1)
n1 - liczebnik dla pierwszej zmiennej
l - liczba wierszy
n2 = k -1
n2 - liczebnik dla drugiej zmiennej
k - liczba kolumn
m = (k - 1)(l - 1)
m - mianownik
l - liczba wierszy
k - liczba kolumn
4.2.1 Zależność preferowanych atrybutów samochodowych od
wykształcenia badanych
Celem przeprowadzonej analizy było zbadanie, czy wybór atrybutów samochodowych zależy od wykształcenia badanych. Oto tabela zawierająca wartości otrzymanych pomiarów.
10
Atrybuty yj |
Podstawo-we |
zawodowe |
średnie |
wyższe |
|
Średnie (w wier-szach) |
samochodowe xi |
|
|
|
|
|
|
Wygląd samochodu i jego elegancja |
3 |
14 |
87 |
59 |
163 |
41 |
Wierność firmie |
0 |
4 |
16 |
19 |
39 |
10 |
Korzystna cena |
4 |
9 |
79 |
44 |
136 |
34 |
Komfort jazdy |
5 |
11 |
70 |
60 |
146 |
37 |
Osiągi trakcyjne |
2 |
5 |
43 |
43 |
93 |
23 |
Niski poziom hałasu |
3 |
10 |
42 |
26 |
81 |
20 |
Obszerne wnętrze |
4 |
13 |
50 |
47 |
114 |
29 |
Bezpieczeństwo |
4 |
15 |
82 |
58 |
159 |
40 |
Pojemność bagażnika |
1 |
1 |
22 |
20 |
44 |
11 |
Pojemność baku |
1 |
4 |
13 |
9 |
27 |
7 |
Instalacja gazowa |
0 |
3 |
6 |
4 |
13 |
3 |
Wtrysk paliwa |
1 |
12 |
19 |
12 |
44 |
11 |
Felgi aluminiowe |
2 |
7 |
15 |
9 |
33 |
8 |
Wspomaganie kierownicy |
5 |
10 |
64 |
47 |
126 |
32 |
ABS |
5 |
13 |
64 |
36 |
118 |
30 |
Automatyczna skrzynia biegów |
1 |
2 |
16 |
10 |
29 |
7 |
Poduszka powietrzna dla kierowcy |
5 |
12 |
61 |
41 |
119 |
30 |
Poduszka powietrzna dla pasażera |
4 |
7 |
52 |
22 |
85 |
21 |
Poduszki powietrzne boczne |
1 |
8 |
23 |
9 |
41 |
10 |
Fabryczne zabezpieczenia przeciwkradzieżowe |
5 |
8 |
34 |
23 |
70 |
18 |
Klimatyzacja |
2 |
8 |
54 |
29 |
93 |
23 |
Szyberdach |
0 |
2 |
13 |
12 |
27 |
7 |
Elektrycznie opuszczane szyby |
3 |
4 |
21 |
15 |
43 |
11 |
Elektrycznie regulowane lusterka |
0 |
2 |
13 |
3 |
18 |
5 |
Centralny zamek |
7 |
10 |
50 |
45 |
112 |
28 |
Komputer pokładowy |
2 |
6 |
11 |
8 |
27 |
7 |
|
70 |
200 |
1020 |
710 |
2000 |
|
Średnie (w kolumnach) |
3 |
8 |
39 |
27 |
|
|
Tab. 4.7
20
Testowane są więc dwie hipotezy zerowe:
H0: Każdy atrybut samochodowy jest jednakowo preferowany przez ankietowanych.
H0: Każdy atrybut samochodowy jest jednakowo preferowany przez ankietowanych z wykształceniem wyższym, średnim, zawodowym i podstawowym.
30
Wykonanie tablicy roboczej zawierającej dane wymagające obliczeń..
Rodzaj zależności |
Suma kwadratów |
Stopnie swobody |
Średni kwadrat (SK) |
Wskaźnik F |
Zależność między preferowanymi atrybutami samochodowymi |
Suma kwadratów zmiennych eksperymentalnych (SKA); suma kwadratów w wierszach |
l - 1 (liczba wierszy minus 1) |
|
|
Zależność między wykształceniem |
Suma kwadratów (SKW); suma kwadratów w kolumnach |
k - 1 (liczba kolumn minus 1) |
|
|
Błąd średniego kwadratu |
Cząstkowe sumy kwadratów (CSK) |
(k-1)(l-1) |
|
|
Ogólna suma kwadratów |
OSK |
kl-1 |
|
|
Tablica 4.8
40
Po określeniu odpowiednich wzorów można przystąpić do ich obliczeń:
1. Ogólna średnia:
![]()
![]()
2. Suma kwadratów zmiennych eksperymentalnych (SKA); suma kwadratów w wierszach (wzór nr 1).
![]()
![]()
Suma kwadratów (SKW); suma kwadratów w kolumnach (wzór nr 2).
![]()
![]()
Ogólna suma kwadratów.
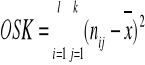
![]()
Cząstkowe sumy kwadratów (CSK).
![]()
![]()
Otrzymane dane umieszczamy we wcześniej przygotowanej tablicy roboczej i obliczamy wskaźniki F.
Rodzaj zależności |
Suma kwadratów |
Stopnie swobody |
Średni kwadrat (SK) |
Wskaźnik F |
Zależność między preferowanymi atrybutami samochodowymi |
14428 |
25 |
|
|
Zależność między wykształceniem |
21866 |
3 |
|
|
Błąd średniego kwadratu |
11344 |
75 |
|
|
Ogólna suma kwadratów |
47638 |
103 |
|
|
Tab. 4.9
50
Dla wskaźnika pierwszej zmiennej o wartości 3,82 obliczamy stopień swobody zarówno w liczniku jak i w mianowniku według wzorów:
n1 = (l - 1); n1 = (26-1) = 25
m = (k - 1)(l - 1); m = (4-1)(26-1) = 75
Wartość krytyczna rozkładu F dla stopnia swobody w liczniku 25 i mianowniku 75 przy poziomie istotności ![]()
= 0,01 wynosi 2,07.
Obliczona wartość 3,82 jest większa od wartości odczytanej z tablicy (3,82>2,07), wobec tego odrzucamy pierwsza hipotezę zerową dla zmiennej eksperymentalnej.
Wniosek:
Zidentyfikowane różnice w wyborze atrybutów samochodowych są istotne statystycznie ze względu na rzeczywiste różnice w preferencjach konsumentów.
Dla wskaźnika drugiej zmiennej o wartości 48,19 obliczamy stopień swobody zarówno w liczniku jak i w mianowniku według wzorów:
n2 = (k - 1); n2 = (4-1) = 3
m = (k - 1)(l - 1); m = (4-1)(26-1) = 75
Wartość krytyczna rozkładu F dla stopnia swobody w liczniku 3 i mianowniku 75 przy poziomie istotności ![]()
= 0,01 wynosi 4,09.
Obliczona wartość 48,19 jest większa od wartości odczytanej z tablicy (48,19>4,09), wobec tego odrzucamy drugą hipotezę zerową.
Wniosek:
Istnieją istotne różnice miedzy osobami z różnym wykształceniem ze względu na ich preferencje w zakresie atrybutów samochodowych
Analiza wariancji wykazała, że różnice w preferencjach atrybutów samochodowych wśród ankietowanych zależą istotnie od samych cech opisujących samochody jak i od poziomu wykształcenia.
4.3 Test Kołmogorowa - Smirnowa
Przy analizowaniu otrzymanych wyników z ankiety, weryfikacji wymaga często istotność różnic między rozkładem empirycznym, otrzymanym z pomiaru porządkowego, a rozkładem oczekiwanym. Narzędziem służącym tej weryfikacji jest m.in. test Kołmogorowa - Smirnowa (test K-S).
W pierwszej kolejności należy skonstruować hipotezę zerową, która zakłada, że nie ma istotnych różnic między rozkładem otrzymanym z próby, a oczekiwanym rozkładem. Weryfikacja hipotezy obejmuje trzy etapy:
Etap I.
Obliczenie skumulowanego rozkładu częstości otrzymanych z pomiaru próby, po przeliczeniu wartości bezwzględnych, na wartości względne.
Etap II.
Obliczenie skumulowanego rozkładu częstości wynikającego z hipotezy H0. Jeżeli hipoteza zakłada brak istotnych różnic między otrzymanymi wynikami z ankiety wówczas proporcje między poszczególnymi kategoriami skali są sobie równe (suma proporcji zawsze równa 1).
Etap III.
Określenie największej różnicy między wartościami skumulowanego rozkładu empirycznego, a wartościami skumulowanego rozkładu hipotetycznego. Największa różnica jest określana jako wartość D Kołmogorowa - Smirnowa. Wartość ta odnajdujemy w tablicy dla odpowiedniej liczebności próby oraz poziomu istotności24.
Wszystkie wyniki liczbowe otrzymane z realizowania kolejnych etapów zapisuje się w specjalnie sporządzonej w tym celu tabeli.
4.3.1 Czy najlepszą porą na zakup samochodu jest wiosna?
Hipoteza zerowa zakłada, że określenie wiosny jako najlepszej pory na zakup samochodu osobowego nie powoduje istotnego zróżnicowania opinii respondentów.
Weryfikacja hipotezy obejmująca trzy etapy dała następujące wyniki.
Kategorie skali |
Liczba odpowiedzi |
Proporcje |
Proporcje skumulo-wane |
Proporcje według Ho |
Skumulo-wane proporcje Ho |
Absolutne różnice proporcji empirycznych i skumulowanych według Ho |
Tak |
53 |
0,265 |
0,265 |
0,2 |
0,2 |
0,065 |
Raczej tak |
53 |
0,265 |
0,53 |
0,2 |
0,4 |
0,13 |
Trudno powiedzieć |
52 |
0,26 |
0,79 |
0,2 |
0,6 |
0,19 |
Raczej nie |
30 |
0,15 |
0,94 |
0,2 |
0,8 |
0,14 |
Nie |
12 |
0,06 |
1 |
0,2 |
1 |
0 |
RAZEM |
200 |
1 |
X |
1 |
X |
X |
Tab. 4.10
Największa różnica między wartościami skumulowanego rozkładu empirycznego, a wartościami skumulowanego rozkładu hipotetycznego wynosi 0,19. Z tablicy rozkładu wartości D Kołmogorowa - Smirnowa odczytujemy, że dla n = 200 oraz przy poziomie ufności ![]()
= 0,01 jest to liczba ![]()
. Ponieważ D = 0,19 > 0,1153 dla![]()
= 0,01, są podstawy do odrzucenia hipotezy zerowej.
Wniosek:
Wybór wiosny jako najlepszej pory na zakup samochodu osobowego powoduje istotne zróżnicowania opinii respondentów. Jest to różnica wyraźnie statystyczna jaki rzeczywista.
4.3.2 Czy kredytowa forma kupna samochodu jest szczególnie atrakcyjna?
Hipoteza zerowa zakłada, że określenie kredytu jako szczególnie atrakcyjnej formy zapłaty za samochód nie powoduje istotnego zróżnicowania opinii respondentów.
Weryfikacja hipotezy obejmująca trzy etapy dała następujące wyniki.
Kategorie skali |
Liczba odpowiedzi |
Proporcje |
Proporcje skumulo-wane |
Proporcje według Ho |
Skumulo-wane proporcje Ho |
Absolutne różnice proporcji empirycznych i skumulowanych według Ho |
Tak |
24 |
0,12 |
0,12 |
0,2 |
0,2 |
0,08 |
Raczej tak |
40 |
0,2 |
0,32 |
0,2 |
0,4 |
0,08 |
Trudno powiedzieć |
40 |
0,2 |
0,52 |
0,2 |
0,6 |
0,08 |
Raczej nie |
61 |
0,305 |
0,825 |
0,2 |
0,8 |
0,025 |
Nie |
35 |
0,175 |
1 |
0,2 |
1 |
0 |
RAZEM |
200 |
1 |
X |
1 |
X |
X |
Tab. 4.11
Największa różnica między wartościami skumulowanego rozkładu empirycznego, a wartościami skumulowanego rozkładu hipotetycznego wynosi 0,08. Z tablicy rozkładu wartości D Kołmogorowa - Smirnowa odczytujemy, że dla n = 200 oraz przy poziomie ufności ![]()
= 0,01 jest to liczba ![]()
. Ponieważ D = 0,08 < 0,1153 dla![]()
= 0,01, nie ma podstaw do odrzucenia hipotezy zerowej.
Wniosek:
Wybór kredytu jako szczególnie atrakcyjnej formy zapłaty za samochód nie powoduje istotnego zróżnicowania opinii respondentów. Nie ma więc istotnych różnic między rozkładem otrzymanym z próby, a oczekiwanym rozkładem.
4.3.3 Czy najlepiej kupić nowe auto z salonu samochodowego?
Hipoteza zerowa zakłada, że chęć zakupu nowego samochodu osobowego z salonu nie powoduje istotnego zróżnicowania opinii respondentów.
Weryfikacja hipotezy obejmująca trzy etapy dała następujące wyniki.
Kategorie skali |
Liczba odpowiedzi |
Proporcje |
Proporcje skumulo-wane |
Proporcje według Ho |
Skumulo-wane proporcje Ho |
Absolutne różnice proporcji empirycznych i skumulowanych według Ho |
Tak |
60 |
0,3 |
0,3 |
0,2 |
0,2 |
0,1 |
Raczej tak |
61 |
0,305 |
0,605 |
0,2 |
0,4 |
0,205 |
Trudno powiedzieć |
34 |
0,17 |
0,775 |
0,2 |
0,6 |
0,175 |
Raczej nie |
33 |
0,165 |
0,94 |
0,2 |
0,8 |
0,14 |
Nie |
12 |
0,06 |
1 |
0,2 |
1 |
0 |
RAZEM |
200 |
1 |
X |
1 |
X |
X |
Tab. 4.12
Największa różnica między wartościami skumulowanego rozkładu empirycznego, a wartościami skumulowanego rozkładu hipotetycznego wynosi 0,205. Z tablicy rozkładu wartości D Kołmogorowa - Smirnowa odczytujemy, że dla n = 200 oraz przy poziomie ufności ![]()
= 0,01 jest to liczba ![]()
. Ponieważ D = 0,205 > 0,1153 dla![]()
= 0,01, są podstawy do odrzucenia hipotezy zerowej.
Wniosek:
Wybór między samochodem nowym, a używanym powoduje istotne zróżnicowania opinii respondentów. Jest to różnica wyraźnie statystyczna jaki rzeczywista.
23 Opracowanie własne na podstawie: S. Kaczmarczyk Badania marketingowe PWE Warszawa'95
24 Opracowanie własne na podstawie: S. Kaczmarczyk Badania marketingowe PWE Warszawa'95
72
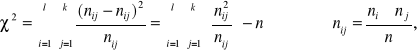
![]()
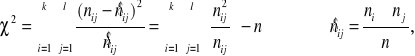
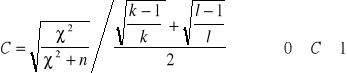
![]()
![]()

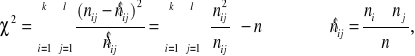
![]()
![]()
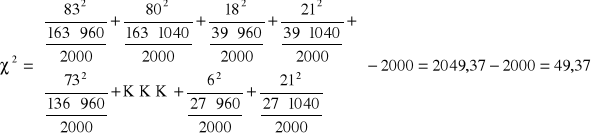
![]()
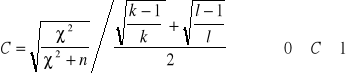
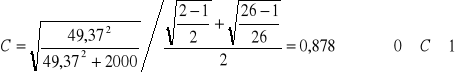
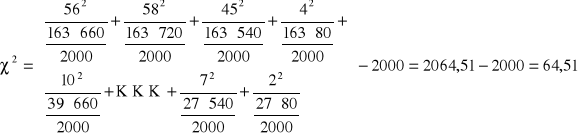
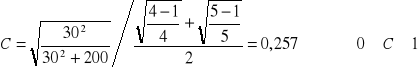
![]()
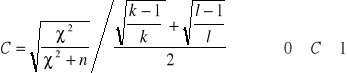
![]()
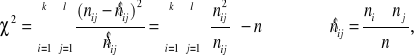
Wyszukiwarka
Podobne podstrony:
takhist, Muhammed ibn Musa Alchwarizmi to perski matematyk, astronom, geograf i kartograf pochodzeni
Co nam dzisiaj podała na kartografii, Geografia, Kartografia i topografia
karto kolos sciaga, Geografia, Kartografia
instr 4, Geografia, Kartografia
obiekty liniowe, Geografia, Kartografia i topografia
instr 4 (1), Geografia, Kartografia
Kartografia notki na egz, studia, Geografia, Kartografia
karto.pojecia, Geografia, Kartografia i topografia
Siatka geograficzna i kartograficzna jako podstawa orientacji na Ziemi, Konspekty lekcji
siatki azymutalne w polozeniu biegunowym, Geografia, Kartografia
obiekty punktowe z uwagami, Geografia, Kartografia i topografia
obiekty powierzchniowe z uwagami, Geografia, Kartografia i topografia
Określenie współrzędnych topograficznych i geograficznych ćw, Geodezja i Kartografia, Kartografia
Geografia jako nauka- definicja i podział geografii mapa i elementy mapy, kartografia
Geografia Geologia Odwzorowania kartograf
Podstawowe terminy geograficzne - material, kartografia
Zadania ortodroma, STUDIA - kierunek GEOGRAFIA, STUDIA, I rok, 2) Kartografia
więcej podobnych podstron