ńĆwiczenie: Odwzorowanie stożkowe proste Ptolemeusza

Przed przystąpieniem do wykonania ćwiczenia należy zapoznać się ze stronami 138-144 z podrozdziału 4.5 w podręczniku Wprowadzenie do kartografii i topografii.

Siatka stożkowa Ptolemeusza w położeniu biegunowym (oś stożka pokrywa się z osią biegunową Ziemi) powstaje w wyniku odwzorowania siatki geograficznej na pobocznicę stożka stycznego z kulą ziemską na wybranym równoleżniku o szerokości geograficznej φ₀ (najczęściej środkowym równoleżniku przedstawianego obszaru). Jest to odwzorowanie równodługościowe w kierunku południków, których obrazami są odcinki linii prostych przecinających się w obrazie wierzchołka stożka W' (ryc. 1). Kąty zawarte między poszczególnymi południkami są pomniejszone w stosunku do oryginału (Δλ'< Δλ). Obrazami równoleżników w tej siatce są łuki kół współśrodkowych względem punktu W'. Równoleżnik styczny o szerokości geograficznej φ₀ ma wymiar rzeczywisty. Pozostałe równoleżniki ulegają wydłużeniu, ale odległości między nimi, ze względu na wierne długości południków, są takie same jak na kuli. Bieguny odwzorowują się także w postaci łuków kół i nie pokrywają się z wierzchołkiem W'. W odwzorowaniu tym można przedstawić całą kulę w wycinku koła, którego wielkość i kształt zależą od doboru równoleżnika stycznego φ₀.

W małych skalach siatkę Ptolemeusza można narysować wykorzystując układ współrzędnych biegunowych (cyrklem i kątomierzem). W większych skalach, ze względu na niedogodności związane z kreśleniem łuków kół bardzo dużymi promieniami wodzącymi, bardziej uniwersalne jest posługiwanie się układem współrzędnych prostokątnych.

Przed przystąpieniem do szczegółowych obliczeń, prowadzący zajęcia wyznacza obszar, który ma być przedstawiony w siatce stożkowej i ustala punkt główny odwzorowania O (φ₀, λ₀), określając równoleżnik styczny i południk główny. Wyznacza również współrzędne punktów węzłowych siatki geograficznej (wielkość oczek siatki) - P_n (φ _n, λ _n) oraz skalę, w jakiej siatka ma być narysowana. W instrukcji omówiony jest rysunek siatki stożkowej prostej Ptolemeusza dla obszaru Polski w skali 1:4 600 000. Za równoleżnik styczny przyjęto φ₀=52° N, a południk główny λ₀=19° E. Oczka siatki zostaną narysowane co 1°. Ze względu na właściwości siatki, takie jak symetryczność względem południka głównego oraz wierne zachowanie długości południków wystarczy obliczyć położenie wybranych punktów węzłowych, leżących na skrajnych równoleżnikach (w przypadku siatki dla Polski na równoleżniku φ_N=55° N i φ_S=49° N, na przecięciach z południkami λ=19°, 20°, 21°, 22°, 23°, 24° i 25° E).

Ćwiczenie realizowane jest w trzech etapach:

I - Przejście z układu współrzędnych geograficznych na kuli ziemskiej na współrzędne biegunowe na płaszczyźnie P (φ, λ) → P' (ρ, Δλ') w założonej skali.

II - Przejście z układu współrzędnych biegunowych na płaszczyźnie na współrzędne prostokątne na płaszczyźnie P' (ρ, Δλ')→P' (x, y).

III - narysowanie siatki stożkowej Ptolemeusza i wrysowanie w nią np. granic Polski, kilku największych rzek oraz wybranych miejscowości.

I. Realizacja pierwszego etapu polega na obliczeniu współrzędnych biegunowych (promieni ρ i kątów Δλ') wybranych punktów węzłowych siatki z uwzględnieniem skali.

a) Obrazem dowolnego równoleżnika jest łuk koła o promieniu oznaczonym jako ρ (ryc. 1). Długość takiego promienia zależy od odległości wybranego równoleżnika φ od równoleżnika stycznego φ₀ (Δφ=φ₀-φ). Ponieważ odstępy między równoleżnikami mają być zachowane zgodnie z rzeczywistością, promień obrazu dowolnego równoleżnika można obliczyć wg wzoru (1):

(1), gdzie:

ρ to promień obrazu równoleżnika o szerokości geograficznej φ,

ρ₀ to promień obrazu równoleżnika stycznego φ₀,

R to promień Ziemi wyrażony w skali (R w skali 1:4 600 000 wynosi ^{637 100 000}/_4 600 000=138,50 cm),

to łuk południka odpowiadający kątowej różnicy szerokości geograficznej między równoleżnikiem stycznym φ₀ a równoleżnikiem φ (Δφ=φ₀-φ). Uwaga! Jeśli zachowamy właściwe znaki wartości szerokości geograficznej, to Δφ=φ₀-φ, będzie miała wartość dodatnią, co oznacza wydłużenie szukanego promienia lub ujemną, co z kolei oznacza skrócenie szukanego promienia w stosunku do promienia ρ₀.

Z ryciny widać, że ρ₀ można obliczyć z wzoru:

(2).

W omawianym przykładzie ρ₀ = 138,5 cm ·ctg 52° = 108,21 cm.

Jeśli do wzoru (1) podstawimy za ρ₀ równanie (2), to otrzymamy:

(3).

W ten sposób znając współrzędne geograficzne punktu głównego O (φ₀, λ₀) i dowolnego punktu P (φ, λ), możemy obliczyć promień wodzący punktu P' (obrazu punktu P) w układzie współrzędnych biegunowych na płaszczyźnie. W omawianym przykładzie obliczymy promienie dla skrajnych równoleżników φ_N=55° N i φ_S=49° N, pamiętając że ρ₅₅ = ρ₀ + R·arc(52° - 55°) = ρ₀ - R·arc 3, a ρ₄₉ = ρ₀ + R·arc(52° - 49°) = ρ₀ + R·arc 3 (R wyrażamy w skali).

b) Pozostaje jeszcze obliczenie kąta biegunowego Δλ', który jest obrazem kąta Δλ, czyli różnicy długości geograficznej między południkiem punktu P, a południkiem głównym (Δλ=λ-λ₀). W każdej siatce stożkowej kąty zawarte między obrazami południków są pomniejszone w stosunku do oryginału (Δλ'< Δλ). Stopień tego zmniejszenia (tzw. zbieżność południków) zależy od szerokości geograficznej równoleżnika stycznego i wyrażany jest w postaci stałej wartości, oznaczonej jako n. Wiedząc, że długości równoleżnika stycznego na kuli 2Πr₀ oraz jego obrazu w siatce n·2Πρ₀ są sobie równe, można porównując te dwa elementy wyznaczyć wartość stałej n, mówiącą o stopniu „ściśnięcia” (zbieżności) południków:

(4), gdzie:

ρ₀ to promień obrazu równoleżnika stycznego φ₀,

r₀ to promień równoleżnika stycznego φ₀.

Chcąc obliczyć różnicę długości geograficznej między obrazami dwóch południków w siatce stożkowej Δλ' należy pomnożyć różnicę Δλ na kuli przez stałą stożkową, n=sin φ₀, czyli:

(5).

W ten sposób możemy wyznaczyć w omawianej siatce położenie obrazu dowolnego punktu na płaszczyźnie w układzie współrzędnych biegunowych P'(ρ, Δλ').

II. Realizacja drugiego etapu polega na obliczeniu współrzędnych prostokątnych wybranych punktów węzłowych siatki P' (x, y) na bazie obliczonych wcześniej współrzędnych biegunowych tych punktów P' (ρ, Δλ'). W tym celu układ współrzędnych biegunowych i prostokątnych nakładamy na siebie osiami X-ów (obraz południka głównego λ₀). Jednocześnie przesuwamy z wierzchołka stożka W' punkt stanowiący początek układu współrzędnych prostokątnych O'( x=0, y=0) o długość promienia ρ₀ równoleżnika stycznego (W' jest początkiem układu współrzędnych biegunowych). Osią Y-ów jest prosta prostopadła do południka λ₀ w punkcie O' (ryc. 1). Ponieważ początki układów współrzędnych nie pokrywają się, należy zastosować trochę odmienny moduł przejścia z jednych współrzędnych na drugie. Na ryc. 1 widać, że:

x = ρ₀ - W'A

Ponieważ W'A = ρ·cosΔλ', można zapisać:

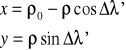
(6).

Posługując się powyższym układem równań (6), można obliczyć współrzędne prostokątne punktów węzłowych siatki stożkowej. Wyniki obliczeń należy zapisać w tabeli dołączonej do arkusza papieru milimetrowego.

III. Realizacja trzeciego etapu polega narysowaniu siatki stożkowej Ptolemeusza w założonej wcześniej skali i wrysowaniu w nią elementów treści geograficznej, zgodnie z zaleceniami osoby prowadzącej ćwiczenia. Na arkuszu papieru milimetrowego A4 w ułożeniu pionowym rysujemy kolorowym tuszem (np. zielonym) osi układu współrzędnych prostokątnych, tak aby początek tego układu O'(0, 0) wypadał na pełnym milimetrze w środku obszaru przeznaczonego na rysunek. Następnie odkładamy wyliczone wartości x i y (z dokładnością 0,01 cm), odnajdując tym samym położenie punktów węzłowych siatki kartograficznej na płaszczyźnie. Naniesione na arkusz papieru milimetrowego punkty węzłowe należy połączyć liniami, uzyskując w ten sposób proste obrazy południków i lekko łukowate obrazy dwóch skrajnych równoleżników (ze względu na bardzo małe krzywizny, najlepiej nadaje się do tego krzywik gięty; cienkie linie siatki, np. o grubości 0,2 mm rysujemy czarnym tuszem). Położenia pozostałych punktów węzłowych można uzyskać dzieląc odcinki odpowiadające 6° łukom południków na sześć równych części. Po narysowaniu obrazów pozostałych równoleżników, siatka powinna zostać ograniczona ramką prostokątną (nieco grubszą od linii siatki, np. 0,5 mm), w której należy opisać wartości południków i równoleżników. W siatkę kartograficzną wrysowujemy wybrane elementów treści geograficznej, np. granice Polski (czarnym tuszem grubością 0,1 mm), kilka największych rzek czy miejscowości, korzystając z map atlasowych (najlepiej w zbliżonej skali).

Siatka stożkowa Ptolemeusza nie zniekształcenia długości w kierunku południkowym, a zniekształcenia wzdłuż równoleżników rosną wraz z odległością od równoleżnika stycznego (odwzorowanego bez zniekształceń). Taki rozkład zniekształceń sprzyja zastosowaniom tej siatki do prezentacji obszarów leżących w średnich szerokościach geograficznych, zwłaszcza w przypadku ich znacznej rozciągłości równoleżnikowej. Połączenie stosunkowo niedużych zniekształceń w pobliżu równoleżnika stycznego z dużą prostotą wykonania sprawia, że siatkę tę często stosuje się w kartografii szkolnej do prezentacji krajów europejskich, m.in. Polski.

TABELA:

Dane: Skala 1: 4 600 000 O (φ₀=52°, λ₀=19°) Δλ = λ - λ₀ Δλ'= sin φ₀Δλ

R=6371 km R_{w skali} = 138,50 cm oczka siatki Δφ×Δλ = 1°×1 °

x = ρ₀ - ρ·cosΔλ'

y = ρ·sinΔλ'

ρ₀ = 138,5 cm ·ctg 52° = 108,21 cm

ρ₅₅ = ρ₀ + R·arc(52° - 55°) = ρ₀ - R·arc 3 =..................

ρ₄₉ = ρ₀ + R·arc(52° - 49°) = ρ₀ + R·arc 3 =..................

Wartości x, y należy obliczyć z dokładnością do 0,01 cm.

Współrzędne geograficzne punktu węzłowego siatki	Δλ [°]	Δλ' [°]	ρ[cm]	x [cm]	y [cm]
P1 (φ1, λ1) P1( 55°, 19°)	0°
P2 (φ2, λ2) P2( 55°, 20°)	1°
P3 (φ3, λ3) P3( 55°, 21°)	2°
...........
...........
...........
Pn (φn, λn) P14( 49°, 25°)	6°

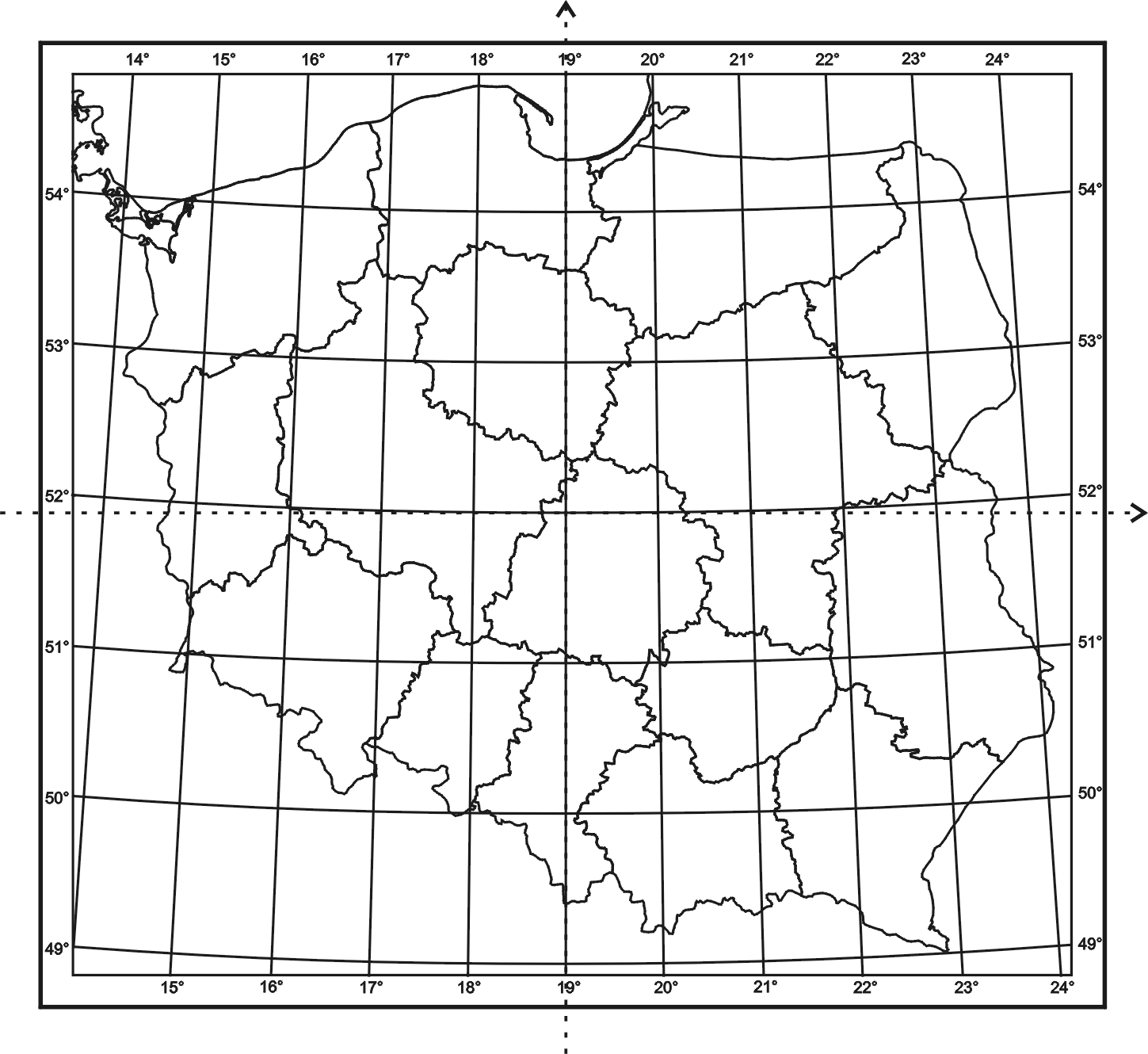
Przykładowa siatka stożkowa Ptolemeusza dla Polski w skali innej niż proponowana w ćwiczeniu:

2

1

---