012

22

(zgodnie z regułą przekory) przeciwnie skierowane do pola B₀. Powstaje w ten sposób ekranowanie diamagnetyczne, którego stała:

(312)

zależy od średniej odwrotności odległości elektronu I od jądra w stanie podstawowym atomu.

B. Niesferyczny rozkład gęstości elektronowej wokół jądra

Jądra ^I3C, ^l9F i ³¹P z elektronami typu 2p mogą być przykładem takich układów. Elektrony p wywołują silne odekranowanie jądra A opisane stałą:

ir_p~-d£-^l<'f^J>lGA«.    (3.1-3)

B

gdzie AE jest średnią energią wzbudzenia elektronu i, Q jest kombinacją elementów macierzy gęstości ładunków atomu A (Q_AA) oraz rzędów wiązań między atomami A i B (Q_AB) ^w przybliżeniu MO dla cząsteczki nie zaburzonej działaniami pola magnetycznego.

Jak widać, stała ekranowania paramagnetycznego zależy nie tylko od stanu podstawowego molekuły. Wpływają na nią wszystkie przejścia elektronowe: a -* a*, a -+ n*, n -*■ <r*, /i -* a*, n n*. Im większa energia wzbudzenia i-tego elektronu, tym mniejsze jest odekranowanie jądra. Z tego powodu dla protonów (rj,^ol[ (wzór (3.1.1)) jest do pominięcia. Dla cięższych jąder (^l3C, ¹⁹F, ^SIP,., .) ten rodzaj ekranowania często dominuje.

Duże znaczenie ma zależność o_p od <r_t^-3> ze względu na związek między r, i gęstością elektronową. Wzrost tej gęstości powoduje bowiem zwiększanie r, i znaczy wzrost ekranowania (spadek wartości a_p).

Następna wielkość we wzorze (3.1.3) (Q_AB) tłumaczy różnice w ekranowaniu jąder atomów, gdy zmienia się krotność wiązań.

C. Gęstość elektronowa a ekranowanie

Dla wielu grup strukturalnie podobnych związków często stwierdza się proste zależności między całkowitą gęstością elektronową (albo np. tylko elektronów a lub u) atomu, a przesunięciem chemicznym jądra tego atomu lub też atomu sąsiedniego. Zwykle jest to spowodowane dominującym udziałem czynnika (r^-i> w zmianach ekranowania jakiegoś jądra w serii podobnych molekuł. Przykładem mogą być jednopodstawione pochodne benzenu, dla których zmiany przesunięć chemicznych jąder ⁱ³C w pozycji para z dużą

\

dokładnością można określić wzorem:

AaC^. = —290AQ_p„_t.    (3.1.4)

Również dla innych klas związków oraz dla innych jąder znaleziono podobne < zależności.

D. Indukowane momenty magnetyczne sąsiednich atomów i wiązań

Duży wpływ na ekranowanie protonów (i innych jąder) mogą wywierać momenty magnetyczne wytwarzane przez pole S₀ w sąsiednich atomach lub wiązaniach chemicznych. Na rysunku 3.1.2 przedstawiono schematycznie wielkość i charakter tego ekranowania dla molekuły H—X, w różny sposób ustawionej względem kierunku pola E₀.

a)    b)

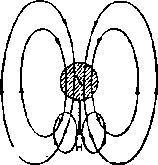
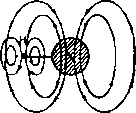
Rys. 3.1.2. Efekt anizotropowy dla cząsteczki X—H: a) — efekt paramagnetyczny, b) — efekt dia magnetyczny.

kienriek pola    kierunek poła

Wielkość dodatkowego pola magnetycznego działającego na jądro H zależy od podatności magnetycznej w miejscu X (y) i może się zmieniać z ustawieniem eząsteczki względem kierunku pola S₀. Mówimy wtedy o anizotropii magnetycznej tego miejsca (atomu, atomów, wiązania), która objawia się zmianą ekranowania jądra H:

Aa = (I -3 cos¹ 9J/12ji/I^j,    (3.1.5)

a

gdzie a oznacza współrzędne x, y, z; y* jest podatnością magnetyczną w miejscu X dla różnych ustawień molekuły względem pola 5₀; 9 jest kątem między momentem magnetycznym wytwarzanym w miejscu X a prostą łączącą H z X; R jest odległością między H i X,

Zjawisko anizotropii występuje też dla układów ze sprzężonymi wiązaniami k. Cząsteczka benzenu jest dobrym przykładem molekuły, w której zewnętrzne