0194

195

§ 3. Podstawowe twierdzenia rachunku różniczkowego

/(a) w pobliżu punktu a z prawej strony i większe od / (b) w pobliżu punktu b z lewej strony. Tak więc a<c<b. Zgodnie z twierdzeniem Fermata otrzymamy wtedy /'(c)=0.

Przechodząc do przypadku ogólnego weźmy dowolną liczbę C zawartą między /'(a) a f’(b); niech na przykład f'(a)>C>f'(b). Rozpatrzmy funkcję pomocniczą <p(x)= =f(x) — Cx, jest ona ciągła i ma pochodną ę\x)=f{x)—C w przedziale <a, b).

Ponieważ ę'{a)=f'(d) — C>0, a ę'(b)=f'(b) — C<0, przeto zgodnie z tym, cośmy udowodnili, istnieje punkt c (a<c<b), w którym

<p'(c) = f'(c) — C=0, tzn. /'(c) = C.

Udowodnione twierdzenie jest bardzo podobne do drugiego twierdzenia Cauchy’ego [82], na mocy którego każda funkcja ciągła przechodzi od jednej wartości do drugiej przyjmując wszystkie wartości pośrednie. Twierdzenie Darboux nie jest jednak wnioskiem z twierdzenia Cauchy’ego, gdyż pochodna funkcji ciągłej sama może nie być funkcją ciągłą.

111. Twierdzenie Rolle’a. U podstaw wielu twierdzeń i wzorów rachunku różniczkowego i jego zastosowań leży następujące proste lecz ważne twierdzenie, które łączymy z nazwiskiem M. Rolle’a (¹).

Twierdzenie (Rolle’a). Niech 1) funkcja f(x) będzie określona i ciągła w przedziale domkniętym <a, b}; 2) istnieje pochodna skończona f'{x) przynajmniej w przedziale otwartym {a, b)\ 3) na końcach przedziału funkcja przyjmuje równe wartości f{a)=f{b).

Wówczas między a i b można znaleźć taki punkt c (a<c<b), że f'(c)=0 (²).

Dowód. Funkcja f(x) jest ciągła w przedziale domkniętym (a, b> i dlatego zgodnie z drugim twierdzeniem Weierstrassa [85], przybiera w tym przedziale zarówno wartość największą M, jak i wartość najmniejszą m.

Rozpatrzmy dwa przypadki:

1.    M=m. Wtedy w przedziale <a,ń> funkcja f(x) zachowuje stałą wartość. Rzeczywiście, nierówność m^f(x)^M daje w tym wypadku f(x)—M dla wszystkich jc; dlatego f'(x)=0 w całym przedziale, jako c można więc wziąć dowolny punkt z przedziału (a, b).

2.    M>m. Wiemy, że funkcja osiąga obie te wartości, ponieważ jednak f(a)—f(b), choćby jedna z nich jest osiągnięta w pewnym punkcie c między a i b. W takim razie z twierdzenia Fermata wynika, że pochodna f'(ć) w tym punkcie znika. Twierdzenie zostało udowodnione.

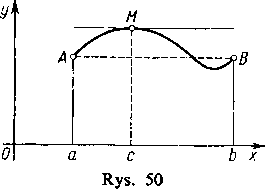
W języku geometrycznym twierdzenie Rolle’a oznacza co następuje: Jeśli skrajne rzędne krzywej y=f (x) są równe, to na krzywej znajdzie się punkt, w którym styczna jest równoległa do osi x (rys. 50).

(‘) W rzeczywistości Rolle wysłowił to twierdzenie tylko dla wielomianów.

(■*) Ciągłość funkcji f (je) w (a, b) założona w 1) wynika oczywiście z 2), ale ani tu, ani dalej nie stawiamy sobie za cel rozbicia założeń twierdzenia na części wzajemnie niezależne.

13*