0196

197

§ 3. Podstawowe twierdzenia rachunku różniczkowego

Udowodnione twierdzenie nosi także nazwę twierdzenia o wartości średniej (w rachunku różniczkowym).

Twierdzenie Rolle’a jest szczególnym przypadkiem twierdzenia Lagrange’a. Zrobione wyżej uwagi dotyczące warunków 1) i 2) twierdzenia pozostają w mocy także tutaj.

Co do interpretacji geometrycznej twierdzenia Lagrange’a (rys. 51) zauważmy, że stosunek

f(b)-f(a)_ CB b-a AC

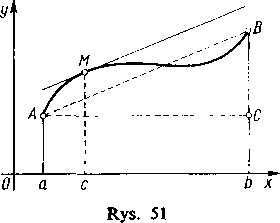
jest współczynnikiem kątowym siecznej AB, zaś f'{c) jest współczynnikiem kątowym stycznej do krzywej y=f(x) w punkcie o odciętej x=c. Tak więc twierdzenie Lagrange’a jest równoważne z następującym: Na luku AB istnieje zawsze przynajmniej jeden punkt M, w którym styczna jest równoległa do cięciwy AB.

Udowodniony wzór

m-m

=/'(c) iub m-m=f\c){b-_a)

nosi nazwę wzoru Lag rangę'a lub wzoru na przyrosty skończone. Pozostaje on oczywiście w mocy także w przypadku a >b.

Weźmy dowolną wartość x₀ w przedziale <a, b} i nadajmy jej przyrost Ax>0 lub Ax<0, taki by x₀+Ax nie wychodziło poza przedział. Zastosujmy wzór Lagrange’a do przedziału <x₀, x₀+zlx> dla Ax>0 lub do przedziału <x₀-Mx,Xo> dla Ax<0. Liczbę c zawartą w tym przypadku między x₀ a x₀+Ax można przedstawić w postaci

c—x₀ + 6Ax, gdzie O<0<1 (¹).

Wówczas wzór Lagrange’a przyjmie postać

=f'(x₀ + 6Ax)

da)

lub

(2)

f(x₀ + Ax)-f(x₀) Ax

Af(x o) =/(x₀ + A x) -f(x₀) =/'(x₀ + 0Ax)Ax (0 < 0 < 1).

Równość ta, dająca dokładną wartość przyrostu funkcji dla dowolnego skończonego przyrostu Ax argumentu, jest naturalnym przeciwstawieniem równości przybliżonej [107, (3a)]:

Af(x o) =/(x₀ + A x) -/(x₀) ~f'(x₀) Ax,

której błąd względny dąży do zera tylko przy Ax nieskończenie małym. Stąd pochodzi sama nazwa wzór na przyrosty skończone.

1

Czasem mówimy, że 8 jest ułamkiem właściwym; nie należy jednak myśleć, że chodzi o ułamek wymierny — 0 może być i liczbą niewymierną.