50338 MATEMATYKA074

140    DI Rachunek różniczkowy

4. PODSTAWOWE TWIERDZENIA RACHUNKU RÓŻNICZKOWEGO.

TWIERDZENIE LAGRANGE'A Jeżeli funkcja f jest ciągła na przedziale domkniętym <a,b> i różniczkowalna wewnątrz tego przedziału, to istnieje taki punkt c €(a,b), że

r_(c)=IMzM.

b ~ a

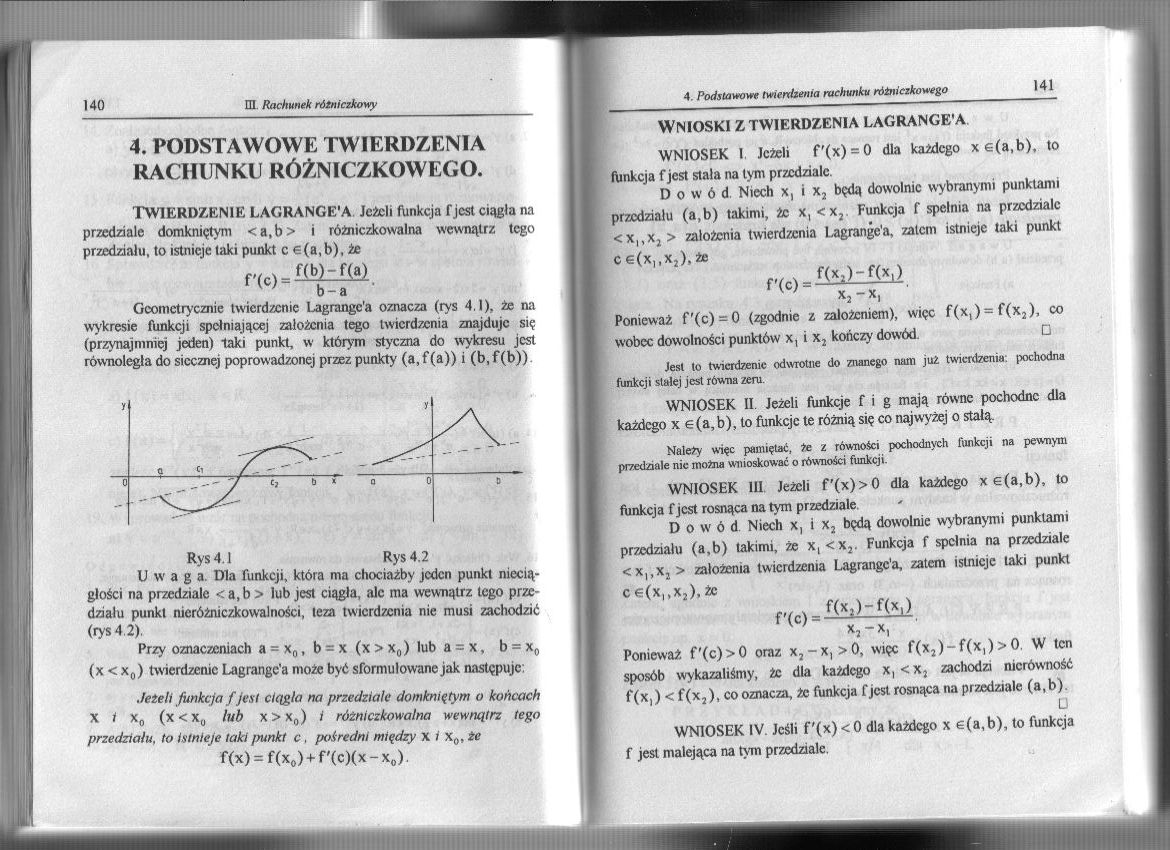
Geometrycznie twierdzenie l.agrangc'a oznacza (rys 4.1), że na wykresie funkcji spełniającej założenia tego twierdzenia znajduje się (przynajmniej jeden) laki punkt, w którym styczna do wykresu jest równoległa do siecznej poprowadzonej przez punkty (a, f (a)) i (b, f(b)).

Rys 4.1    Rys 4.2

Uwag a. Dla funkcji, która ma chociażby jeden punkt nieciągłości na przedziale <a,b > lub jest ciągła, ale ma wewnątrz tego przedziału punkt nieróżniczkowalności, teza twierdzenia nie musi zachodzić (rys 4 2).

Przy oznaczeniach a = x₀, b = x (x > x₀) lub a = x, b = x₀ (x < x₀) twierdzenie Lagrangea może być sformułowane jak następuje:

Jeżeli funkcja f jest ciągła na przedziale domkniętym o końcach X i x₀ (x<x₀ łub x>x₀) i różniczkowalna wewnątrz tego przedziału, to istnieje taki jninkt c, pośredni między \ i x₀, że f(x) = f(x₀) + f'(c)(x-x₀).

Wnioski z twierdzenia lagrange a

WNIOSEK I. Jeżeli f'(x) = 0 dla każdego x€(a,b), to funkcja f jest stała na tym przedziale.

D o w ó d. Niech x, i x₂ będą dowolnie wybranymi punktami przedziału (a,b) takimi, że x, <x₂. Funkcja f spełnia na przedziale <x,,x₂> założenia twierdzenia Lagrange’a, zatem istnieje taki punkt c €(x₁,x₂), że

_{P(c) =} ^f(^x₂)-^f(^xi)

x₂-x,

Ponieważ f'(c) = 0 (zgodnie z założeniem), więc f(x,) = f(x₂), co wobec dowolności punktów x, i x₂ kończy dowód    D

Jesl lo twierdzenie odwrotne do znanego nam już twierdzenia. pochodna funkcji stałej jest równa zeru.

WNIOSEK II. Jeżeli funkcje f i g mają równe pochodne dla każdego x € (a, b), to funkcje te różnią się co najwyżej o stałą.

Należy więc pamiętać, Ze z równości pochodnych funkcji na pewnym przedziale nie można wnioskować o równości funkcji.

WNIOSEK III Jeżeli f'(x)>0 dla każdego x €(a,b), to funkcja f jest rosnąca na tym przedziale

D o w^r ó d Niech x, i x₂ będą dowolnie wybranymi punktami przedziału (a,b) takimi, że x,<x₂. Funkcja f spełnia na przedziale <x,,x, > założenia twierdzenia Lagrangea, zatem istnieje laki punkt C€(x,,x₂),że

x₂-_X,

Ponieważ f'(c)>0 oraz x₂-x, >0, więc f(x₂)-f(x,)>0. W ten sposób wykazaliśmy, źc dla każdego x, < x₂ zachodzi nierówność f(x,) < f(x₂), co oznacza, że funkcja f jest rosnąca na przedziale (a,b).

□

WNIOSEK IV. Jeśli f'(x) < 0 dla każdego x e(a,b), to funkcja f jest malejąca na tym przedziale.