0440

441

§ 4. Zamiana zmiennych

Za pomocą znalezionych wzorów możemy im nadać postać

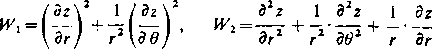
2) Przejście do współrzędnych sferycznych. Rolę analogiczną do roli współrzędnych biegunowych na płaszczyźnie grają w przestrzeni współrzędne sferyczne p, <p, 8. Współrzędne prostokątne x, y, z związane są z nimi wzorami

x=psin <pcos8, y = psin ęsin8, z=pcos<p.

Przypuśćmy, że trzeba przekształcić przechodząc do zmiennych p, q>, 8 wyrażenia

w których u jest pewną funkcją punktu w przestrzeni.

Przekształcenie wykonamy w dwóch etapach przyjmując najpierw x = r cos 8. y= r sin 8 i pozostawiając z bez zmiany, a następnie przyjmując z=p cos q>, r = p sin p i pozostawiając bez zmiany 8. Dzięki temu będziemy mogli posłużyć się wynikami z przykładu 1).

Na przykład dla drugiego wyrażenia otrzymujemy

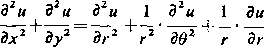
Wyrażeniu w nawiasach możemy, korzystając znowu z przykładu 1), nadać postać

8²u    1 3² u    1 Bu

Bp²^ p² 8<p² ^ p Bp

dalej

Bu    Bu cos ę Bu

Podstawiając znalezione wyrażenia otrzymujemy ostatecznie

Analogicznie znajdujemy

Wi =

3) Wykazać, że wyrażenia W_l i W₂ zachowują swoją formę przy przejściu od współrzędnych prostokątnych do dowolnych innych współrzędnych prostokątnych

x' = a_t x + bt y + Ci z ,    y'= a₂x + b₂ y+ c₂ z , z'= a₃ x +b₃ y + c₃ z ,

gdzie współczynniki a,, b,, c, spełniają znane zależności

gdy i-j, gdy f'#y.

(26)