046 (9)

Równania trygonometryczne

Od obydwu stron odejmujemy 1. następnie obie strony dzielimy przez 2.

Uzyskujemy równanie elementarne.

2 sin (x - 5) = 2 - 1 2 sin (jc - 5) = 1 1:2 sin (jc — 5) = —

n

x - 5 = x₀+ 2kn lub jr - 5 = n-x₀ + 2kn, k e C

Czyli

Teraz szukamy takiego kgta x_;, dla którego

K _,

x - 5 = 7 + 2kn 6

lub

x-5 =

rt

- 7 + 2/rw = — tt + 2kn, k 6 6

sinus ma wartość Jest nim §

2 o

Wstawiamy znalezioną wartość -r do wzorów rozwiązań, pamiętając, że zamiast x wpisujemy

C

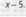
Teraz z każdego równania wyliczamy ..    ,    ...    .    ,

°    ^J    J    Następnie uzyskane równania liniowe przekształ-

camy tak, aby uzyskać x.

_x — 5 ₌ _ + 2kn k G C    W tym ^{celu w} obydwu przypadkach przenosimy

(j    *    -5 na prawą stronę, zmieniając znak na prze

ciwny.

x = 5 + 7 + 2kn, k e C 6

x - 5 = 7 n + 2kn, k e C 6

x = 5 + - k + 2kn, k e C 6

Odpowiedź

C

x - 5 + 7 + 2kn lub x = 5 + 7 it + 2kn, k e 6 6

ZADANIE 8

„ ...

Rozwiąz równanie: cos x = —

46