0478

479

§ 2. Prosta styczna i płaszczyzna styczna

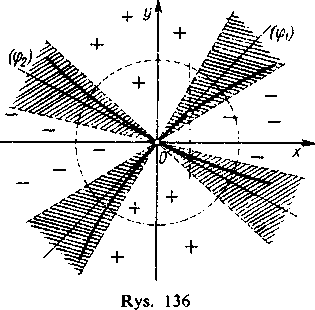
Weźmy teraz dwa dowolnie małe obszary kątowe zawierające wewnątrz proste {ę₂) i (ę₂), a mianowicie dwie pary kątów wierzchołkowych — zawarte między prostymi —c) i (>!+£) oraz między prostymi (<p₂-c) i (ę₂ + e) (na rys. 136 kąty te są zakreskowane). Jeśli weźmiemy koło o dostatecznie małym promieniu r, i o środku w początku układu, to możemy twierdzić, że po odrzuceniu obszarów kątowych zawierających proste (ę_y) i (ę₂) koło to rozpada się na dwa obszary kątowe, w każdym z których funkcja F(x, y) zachowuje znak — w jednym jest dodatnia, w drugim ujemna (patrz rysunek 136). Istotnie, ponieważ przy zmianie kąta ę poza przedziałami (ę?j — £, ę_y+E) i {<p₂ — £> <Pi+ć) trójmian (18) jest stale różny od zera, więc jego wartość bezwzględna jest stale większa od pewnej dodatniej liczby m_t. Z drugiej strony, dla dostatecznie małego p wyrażenie oc_u cos² <p + 2a₂₂ cos ę?sin f + a₂₂ sin² <p ma wartość bezwzględną mniejszą od m_Ł. Stąd właśnie wynika potrzebny nam wniosek (porównaj rozumowanie w ustępie 197, 1°).

Rozpatrzmy teraz dwa zakreskowane wycinki koła leżące w jednej parze kątów wierzchołkowych, na przykład te, które są ograniczone prostymi (<p₂ — s) i (<p₂ +£).

Ponieważ na tych prostych funkcja F(x, y) ma przeciwne znaki, więc na każdym pionowym odcinku łączącym te proste znajduje się punkt, w którym funkcja F(x, y) jest równa zeru, to znaczy punkt badanej krzywej. Wynika to ze znanej własności funkcji ciągłych [80], którą to własność przy ustalonym x musi mieć także i funkcja F(x, y) zmiennej y (¹).

Tym samym wewnątrz każdej pary zakreskowanych kątów wierzchołkowych leży gałąź krzywej przechodząca przez początek układu. Przy tym na zewnątrz tych kątów, ale wewnątrz koła, nie ma punktów krzywej. Ponieważ £ jest dowolne, więc gałęzie te są oczywiście w początku układu styczne odpowiednio do prostych {(Pi) i (ę>₂).

Pozostaje jeszcze nie rozstrzygnięte pytanie, czy na wspomnianym pionowym odcinku istnieje tylko jeden punkt, w którym F(x, y) — 0? Gdyby takie punkty były dwa, to z twierdzenia Rolle’a wynikałoby, że na tym odcinku leży między nimi punkt, w którym F'_y (x, y) = = 0. Zatem jednoznaczność będzie udowodniona, gdy pokażemy, że przynajmniej w dostatecznie małym otoczeniu początku układu i przy tym wewnątrz zakreskowanego kąta równość taka jest niemożliwa.

Przypuśćmy, że jest przeciwnie. Mamy zatem F'_y(x„, y„) = 0 dla pewnego ciągu punktów

y_n

{(jc„, y„)}, w którym x„-»0 i —>tg tp_l = t₁. Zastosujmy do funkcji F (x, v) wzór na przy-

1

Porównaj dowód twierdzenia I z ustępu 206 o istnieniu, funkcji uwikłanej.