1 7d pole sil potencjalnych

2 porównania wielkości przv tvch samych różniczkach współrzędnych dostaniemy

_F . JtL

dx dli

^F» = ^— aT dy

_F = JJŁ

dr.

(2.28)

Istnieje krótki zapis symboliczny tego związku wektora sil działających od pola z polem skalarnym energii potencjalnej

F(#_; y, z) — -grad U(x, y, z).    (2.29)

Do szczegółowej dyskusji tego wzoru wrócimy w elekt rostatyce bo matematyczny opis obu pól (grawitacyjnego i elektrycznego) ma bardzo duże podobieństwo. Tutaj rozpatrzymy zagadnienie tylko w jednym wymiarze gdzie odpowiednie równanie ma prostą postać

(2.30)

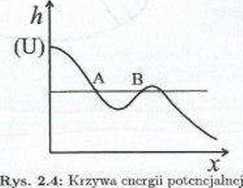
Na rys. 2.4 pokazano profil przekroju terenu zawierający dolinę na żboczu góry. Wysokość h terenu w funkcji współrzędnej x jest jednocześnie funkcją energii potencjalnej w funkcji tej współrzędnej ponieważ

U{$) = myh(x).    (2.31)

Na rysunku zaznaczono poziom energii ciała (np. kuli) umieszczonego w obszarze doliny. Kiedy ciało jest w punkcie A na zboczu doliny, pochodna energii potencjalne po współrzędnej jest ujemna i po uwzględnieniu znaku ujemnego we wzorze (2.30) siła ma znak dodatni czyli zgodny z kierunkiem osi x. W punkcie B sytuacja będzie przeciwna — siła będzie spychała dało w lewo, znowu w dół zbocza doliny. W przypadku kiedy praca jest wykonywana siłami wewnętrznymi układu, energia potencjalna układu będzie zmniejszała się i ciało będzie zyskiwało na prędkości. (Jeśli działać będą tvlko siły zachowawcy? pplą energia potencjalna ciała będ2ie się zamieniają PA    -kj^yCT.a^,,f=uma energii zwana energią mechaniczną będzie pozostawała stała. By

to uzasadnić napiszmy

dr\

'^{= d£}*'    (2-M)

—tlU = Fdr = (m—-)(wU) mv> d t

Stąd już prosto wynika, że

" b, )    (2 33)

czyli suma energii kinetycznej i potencjalnej nazywana energią mechaniczną pozostaje stała. Jest to szczególna postać zasady zachowania energii.

21