132

Wykorzystując warunki początkowe, że dla t » 0 masa m jest wychylona o f₀, a jej prędkość w tej chwili wynosi

v

o

- o,

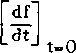
otrzymujemy ostatecznie rozwiązanie w postaci:

(12.12)

f =* f cos pt. o

Natomiast okres drgań masy m wynosi:

T

2 TC p

2 TC

12.3. DRGANIA BELKI Z MASĄ SKUPIONĄ W ŚRODKU PRZY UWZGLĘDNIENIU MASY BELKI

Chcąc uwzględnić masę własną belki w obliczeniu 'drgań, należy do wyliczonej w p. 12.2 energii kinetycznej E^ i energii odkształcenia E_p dodać energię kinetyczną belki. Obliczamy ją przy założeniu, że masa belki jest rozłożona równomiernie, a postać ugiętej osi belki w czasie drgań jest taka sama, jak w przypadku statycznego obciążenia jej siłą skupioną w środku. Przemieszczenie y dowolnego punktu belki Opatrz rys. 12. l) przy statycznym działaniu siły P przyłożonej w środku belki otrzymamy z rozwiązania równania różniczkowego osi ugiętej belki:

E I y" » - M .    (12.13)

^z    g

W rozpatrywanym przypadku w przedziale 0 4 x 4 ^ ^momeTlt gnący określony jest równaniem:

M = P x. g 2

Po podstawieniu wyrażenia na Mg do równania (l2.13) i dwukrotnym scałko-waniu otrzymujemy:

E ^Tzy =    ^ P x³ + C_x x + C₂.    (12. U)

Po podstawieniu warunku brzegowego y - 0 i warunku wynikającego z sy-metrii:    ^X=0

(y' )_{x =} i_ = °»

2

132