176

W przypadku parowania cieczy równanie Clapeyrona ma postać

ŚR =    ^    (63)

dT    T{v" - v')

W obszarze, w którym objętość właściwa pary nasyconej suchej jest znacznie większa od objętości cieczy wrzącej, a do opisu pary nasyconej można wykorzystać równanie Clapeyrona, równanie (63) przekształca się do postaci równania Clapeyrona-Clausiusa

dhip ₌ ^Aic-_g(^T)    (_6-4)

dT rt²

w którym

^c-_s(T) - A«_e_,₍r₀)

T

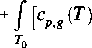
-c_c(T)]dT

(6.5)

Rozważa się układ jednoskładnikowy i dwufazowy (ciecz-para) rozdzielony powierzchnią zakrzywioną. Warunkami równowagi między tymi fazami będzie równość temperatur oraz równość potencjałów chemicznych w obu fazach. Wystąpi natomiast różnica pomiędzy ciśnieniami w obu fazach. Różnica ta nosi nazwę ciśnienia powierzchniowego. Wykazuje się łatwo, że w przypadku kulistego kształtu kropli o promieniu r, różnica ciśnień wynosi

Pb =

2 o r

(6.6)

gdzie o napięcie powierzchniowe [N-m¹].

Z warunków równowagi fazowej otrzymuje się dla tego przypadku, iż

V_cdp_c = vdp_g

dp_c = -2-dp v *

(6.7)

Jeżeli do tego założy się, żę objętość właściwa cieczy zmienia się nieznacznie, a w przypadku pary można skorzystać z równania Clapeyrona, to po całkowaniu po krzywiźnie od płaskiej powierzchni, nad którą para ma ciśnienie /?„

i

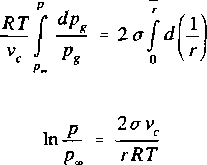
(6.8)

otrzymuje się, że (6.9)

Wynikający ze wzoru (6.9) wzrost ciśnienia pary zawierającej krople cieczy prowadzi do opóźnienia jej kondensacji.

176