44139 spektroskopia020

40

Równanie oscylatora dla tego przypadku ma postać

m*x + m*yx = — eS₀e~^icot,    (4.5)

gdzie m* jest masą efektywną nośników, tłumienie ruchu y opisuje wszystkie procesy rozpraszania y = 1/t, t jest czasem relaksacji (średni czas między kolejnymi zderzeniami elektronu). Człon m*o>ox w równaniu (4.5) nie występuje, ponieważ dla elektronów swobodnych

co0 = 0. Rozwiązanie równania (4.5) ma postać
x = e<?oe^-j“^ł[m*(c0^2-H(uy)]^-1.	(4.6)
Polaryzacja wyraża się jako
D xr -4nNe^2 E0e~^ical p = -Nex =-.--f——, m eir + icoy	(4.7)
gdzie N — koncentracja swobodnych elektronów. Ponieważ P — (e—1)£, dlatego
. . 4nNe^2 1 «(co) = 1--;--j——. ni co* + icoy	(4.8)

Fala elektromagnetyczna oddziałuje w krysztale nie tylko ze swobodnymi elektronami, ale także z siecią oraz z elektronami walencyjnymi, co prowadzi do wystąpienia przejść międzypasmowych. Oddziaływania te uwzględnia się przyjmując, że prowadzą one do przenikalności elektrycznej stanowiącej tło dla procesów związanych ze swobodnymi elektronami. Zakłada się, że jest ona stała i wprowadza do wzoru (4.8) jako £_ro zamiast 1.

Teraz wzór ten można zapisać w postaci

gdzie: coj =

47t Ne²

s(co)

CD

² + icoyj'

(o²p

— częstość plazmowa.

(4.9)

(4.10)

Części rzeczywista i urojona mają następujące postaci:

fi^Ct)) = £

CDt

co² + y²

)■

£₂(0>) =

^£«^py co(tu² + y²)'

(4.11)

(4.12)

Wkład swobodnych nośników do części rzeczywistej funkcji dielektrycznej jest ujemny, co jest związane z tym, że nośniki swobodne poruszają się w fazie przeciwnej do pola elektrycznego.

Można zauważyć, że £₂(co) jest proporcjonalne do parametru tłumienia y, tak samo jest ze współczynnikiem absorpcji ot

(4.13)

(4.14)

(4.15)

nc(co² + y²)

Dla małych częstości co « y otrzymamy

_ 4nNe² K ncrrfy'

co możemy dalej zapisać jako

4na

a =-,

nc

gdzie

Ne² 1 <r = ——-m y

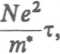
otrzymując znane wyrażenie na przewodnictwo elektryczne.

Zwykle parametr tłumienia y jest mały w porównaniu z częstością plazmową co_p. Wtedy dla co » y otrzymujemy:

	p _^£=0	(4.16)
oraz	, . C0£, £_ coiy 1 ,, a(co) = —- « ——* ~ A^2. cn cn co^2	(4.17)
Okazuje się,	że zależność
	ot = AX^2 4- p,	(4.18)
gdzie	e^3N 1 ~ 47t^2c^3n <^) <m*>’	(4.19)

można uzyskać uśredniając kwantowo-mechanicznie różne procesy absorpcji na swobodnych nośnikach «/i> i <m*> — średnia ruchliwość i masa efektywna).