4522

70

Macierze i wyznaczniki

Jedynym rorwiąraniein lego ikłida jat czwórka liczb • ■ I, b *= O, c m 3, d m 2. Roi wiązaniem m»<iufgo równani* jest talem macierz

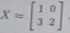
c) Niecli X

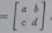
gdzie a,ł,r,ił e C, będzie szukaną macierzą.

Wtedy z warunku

8p    ■ plltellSi .

otrzymamy układ równań

a^ł - <f^ł a 0 ab + W = 0 flC + frf a 0

bc + d* « i

{

•* + bc •b + W sc + rd *e +

który jest równoważny układowi

Możliwe są zatem dwa przypadki a — d lub a = — d. Jeżeli a ts d, to ab = ae = 0 i *e = 1 - s^J. Wtedy dla u = 0 mamy *c = 1. Macierz X jest więc postaci

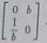
Gdy sftO. lo ł ■ r ■ 0 i wtedy a = 1 lub a m -|. W tym przypadku macierz X jest postad

^■k‘v IBS

Natomiast w przypadku drugim, gdy a = -d, otrzymamy zależność leul- / Wtedy dla ż = 0 mamy u = 1 lab a = -1, przy czym e jest dowolne. Jeżeli jednak * fi 0, to 1-a³ _w . _v .

^c ■ —j—■ Macierz a jest więc w tym przypadku odpowiednio post aa

■■I li

Zatem rozwiązaniem równania są tylko macierze X postaci

n o]	f-i ol	r. -, I	fi o]
(e-jJ-	1 **}'		[o.J- [

gdzie a,b,c € C b jć 0.

• Przykład 6.6

Korzystając s własności działań z macierzami oraz własności operacji transpono-waoia macierzy uzasadnić podane tożsamości:

a) (A - By = A^r - B^T, gdzie A i B są macierzami tych samych wymiarów;

71

Szósty tydzień - przykłady

b) A¹ - B³ = (A- B)(A + B), gdzie A i B przemiennymi macierzami kwadratowymi tych samych stopni.

Uwaga. Mówimy, ie macierze .4 i B są przemienne, gdy spełniają warunek

AB = BA.

Rozwiązanie

a)    W dowodzie wykorzystamy następujące własności transpozycji macierzy: (4+ B)^T m A^T + B^T oraz (o.4)^T = a (A^T) , gdzie A i B są macierzami tych samych wymiarów, a o jest liczbą rzeczywistą lub zespoloną. Mamy

(A - Bf = [A + (-1 )B)^T mA^T + ((-l)Bf = d^T + (-fł^r) = a^t - B^T.

b)    W dowodzie wykorzystamy wtór (4 ± B)C = AC £ BC, gdzie A, B są macierzami wymiaru n x m, a C jest macierzą wymiata m x k oraz wzór D(A £ B) = DA £ DB, gdzie D jest macierzą wymiaru / x n. Dla macierzy przemiennych mamy

(A - B)(A + B) = A(A r B) — B(A + B) = '(A³ + AB) - (BA + B³)

= A³ + AB - AB - B³ = A* - B*.

• Przykład* 6.7

Zbadać, czy istnieje macierz kwndratowa X stopnia n taka, że dla każdej macierzy kwadratowej A tego samego stopnia prawdziwa jest równość /IX = A^T.

Rozwiązanie

Gdy n ss 1, to szukana macierz ma postać X - fl). Pokażemy, że dl* n ? 2 nie istnieje taka uniwersalna macierz X. Niech X =    oznacza szukaną macierz oraz niech

A = fai,]„_n oznacza dowolną macierz. Wtedy* powinna być spełniona równość

•ił ^fll*		*11 *1J v **«		On 021 ••• ?"l
aji njz ••••■ •*		*21 *22 ••• *2n	CS;	OiJ OW ^a*»2
a«i 0n2 .*. .		. *»1 *«2 ... *»« .		. U]n «!• -

Przyjmijmy, że macierz A ma następującą postać

1    1    ...    1

0    0    ...    0

. 0    0    .,ź)    0    .

Wtedy w wyniku pomnożenia pierwszego wiersza macierzy A pnez drugą kolumnę macierzy X otrzymamy równość

*12	+ *22+ ••• + *«»
Przyjmując teraz, ie macierz A ma postać
	• 1 1 ... 1 ■
	1 o ... o
	, 0 0 ... 0 ,