analiza01a

Międzywydziałowe Studium Informatyki i Ekonometrii Analiza matematyczna Zadania przygotowawcze do egzaminu

1. Wyznaczyć kresy zbioru

a) A — {i S R : nx² — (2n² + l)x + 2n = 0 , n € N}

b) A = {x € Q : x = - ; -q < p < 6 , q € N}.

2.

a)

3.

Stosując definicję granicy ciągu wykazać, że

4"

c) lim —- = 0.

n—>oo 7x|

n² + 4n 1    .    n³ + 2n - 4

lim    7,— -= -    b) lim ——-= oo

n—><» 3n² — 2n — 1    3    ⁿ—*⁰°2n² —n + 11

Obliczyć granicę ciągu {x„} punktów z E⁴, jeśli

\/4ⁿ + 3" - n ;

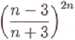
1 + 4 + 7 + ... + 3ra + 1 n² +1

/ n³ - 2 y 2n³ + n

4. Zbadać ciągłość i różniczkowalność funkcji

- dla x ± 0

x

4 dla x = 0

a) f(x)

(x³ cos — dla x ^ O x

O dla x = O

5. Zbadać przebieg zmienności funkcji

a)    f(x) = ln²x — lnx , x>0

b)    /(x) = x²e~^2x , x 6 R

1

c) /(x) = (x + 2)e^x , x € (—oo;0) U (0;oo).

6.    Wyznaczyć najmniejszą i największą wartość funkcji /(x), gdy

a)    /(x)=x³lnx dla

b)    /(x) = x²e^-21 dla x € [O, oc)

c)    /(x) — x^2x dla x € lj.

7.    W zależności od wartości parametru k € R podać liczbę rozwiązań równania

a) In x = kx    b) e^x = kx².

8.    Znaleźć wartości a i b, dla których funkcja /(x) = alnx + bx² + x dla x € R ma ekstremum w punktach Xj = 1 i x₂ = 2.

9.    Zbadać zbieżność danego ciągu funkcyjnego w metryce sup w odpowiedniej przestrzeni

a) . fn(x) = ~^X- - w C([0,2]) iw A/([0,oo))

X* ~h Tl

b) . /„(x) = sin- w A/([0, oo))    c). /_n(x) = i/x²+- w C([0,3])

n    y n

d) . /n(x) = x²"c~⁷¹¹ w M([0,oo)).