CCF20090604000

Sieci Bravais’a

Przypomnienie

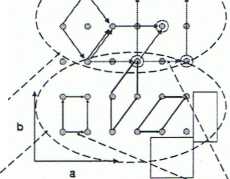
Komórka elementarna - równolegtościan obejmujący najmniejszy powtarzający się periodycznie fragment sieci przestrzennej. Krawędzie komórki są zgodne z osiami układu krystalograficznego. Długości krawędzi komórki są równe długościom translacji sieciowych a, b, c i tworzą między sobą kąty a, p, y

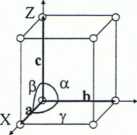
a = Z (b,c) P = Z (a,c) y = Z(a,b)

Komórki elementarne dzieli się na:

prymitywne

węzły znajdują się jedynie w narożach komórki

centrowane

węzły znajdują się nie tylko w narożach, ale również na ścianach lub w środku komórki

V

10. A Rybarczyk-Pirek

Skąd pojawiają się komórki centrowane?

10. A. Rybarczyk-Pirek    2

Sieci przestrzenne różnią się symetrią, którą opisują grupy punktowe. Każda grupa punktowa przypisana jest do określonego układu krystalograficznego.

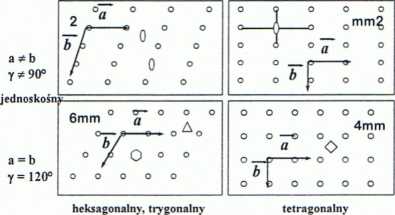
a * b y = 90° rombowy

a = b y = 90°

Nie zawsze trzy najkrótsze translacje bazowe sieci a b są zgodne z kierunkami osi symetrii danej sieci.

10. A. Rybarczyk-Pirek

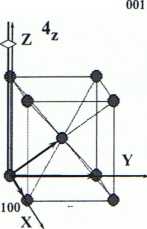
Jeśli sieć charakteryzuje się symetrią obrotową, wygodnie jest wybrać kierunek osi symetrii jako kierunek jednej z osi własnego układu odniesienia sieci ( X, Y, Z )

Np. przy symetrii tetragonałnej kierunek Z (wyróżniony) powinien kierunkiem osi czterokrotnej 4. Pozostałe dwa kierunki (X,Y) wybiera się jako prostopadłe do wyróżnionego (Z) i kąty pomiędzy osiami powinny są proste (a = p = y = 90°).

Translacje sieciowe

nie są wtedy możliwymi najkrótszymi 000 translacjami bazowymi, a komórki mogą zawierać więcej węzłów.

Dodatkowe węzły posiadają wskaźniki    tetragonaina komórka

ułamkowe.    centrowana

10. A.Rybarczyk-Pirek    4

ViV

Typy komórek elementarnych i sieci przestrzennych

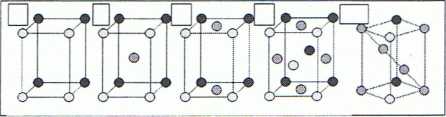
P    I    C (A, B)

prymitywna    wewnętrznie    dwustronnie

Z=1000    centrowana    centrowana

(Innercentrierte)    Z=2;

Z=2;    000 '/₂ V₂ 0

000 Vi Zi '/a

R

centrowana trygonalna (romboedryczna)

Z=4; 000    Z=3; 000 2/3 2/3 1/3

'/a '/a 0 '/a 0 ‘/a    1/3 2/3 2/3

0 '/a ‘/a

Baza komórki: wskaźniki najmniejszej liczby węzłów koniecznych do odtworzenia całej sieci zbudowanej z rozważanego rodzaju komórek. Zawartość komórki - suma węzłów przypadających na komórkę elementarną.

10. A. Rybarczyk-Pirek    :

Wybór komórki elementarnej oraz osi własnych sieci

Spośród wielu różnych możliwości w celu charakterystyki sieci należy wybrać komórkę:    ------

>    najprostszą (zawierającą /'& ^ ₀ (gy......<g)"

najmniej węzłów,

0    najmniejszej bazie)

>    najmniejszą

(o najkrótszych krawędziach

1    kątach najbardziej

zbliżonych do 90°)    /

... /

>    o najwyższej    /

symetrii    /

komórki centrowane ^x

/'

komórki prymitywne /    komórki zgodne z symetrią-ii

10. A. Rybarczyk-Pirek mm2    6

1