DSC07304

30

Liczby zespolone

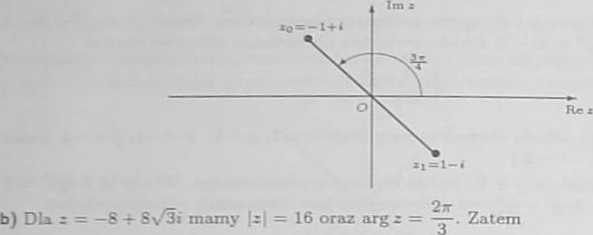
V—8 + 8 V5i= < v^16

: * = 0,1,2,3

f,.. ¥^+2fcr'

lak więc dla k = 0. L. 2,3 mamy odpowiednio

§=² («* f+^iafa f) =² (ir+1¹) = '^/5+i-

*^ł=2(““T^+iain¥)⁼²(^_5 ⁺ ^=^_1+V5<*

^=a=2(“⁸T^+isinT) ^{= 2}(^-^^-?) =

^I,=2(^c“¥⁺ⁱ⁸ⁱⁿT) ⁼²(l~    ^

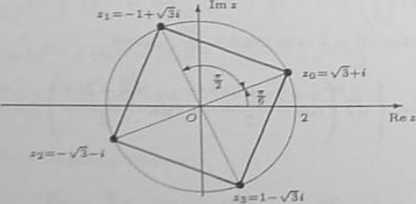
Stąd

V-8 + 8^3i = {V3 + i,-l + V3i,-V3 - i,l - S»} . e) Dla * = 1 mamy jzj = 1 oraz argi = 0. Zatem

-yr={yi(_c

0+2ifar

6

+ t«in

P+-2/;tt\ 8 /

8

t = 0,1,

6}.

Przykłady

31

Tak więc dla fc = 0,1,2,3,4,5 mamy odpowiednio

= 1 (cosO + isinO) = 1,    =i = 1 (^C08^ ^{+ iain}|) = | + ^i,

/ Ir . -2śA 1    ,    -J&i    * #} t HI. \

IJ =    1    ( cos — +1 Sin — J    = —- +    —1,    zj = Hcosir + ismir) = -1,

/ 4ir , . - 4rr\    S 1    S/5.    _, / 5ir . 5ir\ 1    y/3.

_I4 =    1    (co_ST+.sm_Tj    = -2--2'».    » ^co.~_+lsin~)

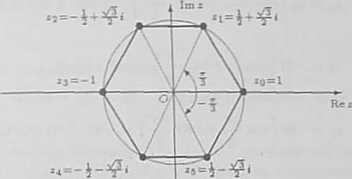
Ostatecznie

J, ¹ , A l.A- i 1    V5. 1    V3.\

^=\^l-2⁺T’^2⁺‘T’" “j - -r*2 r‘j•

• Przykład 1.19

Odgadując jeden z elementów podanych pierwiastków obliczyć pozostałe elementy tych pierwiastków:

a) 7(3-5i)^J; b) ^f+1⁵; c)

Rozwiązanie

W rozwiązaniu wykorzystamy wzór wyrażający elementy zbioru

V* = (zo, *i_t • - • i *n-l}

w zależności od wybranego pierwiastka zo, przy czym argument główny zo niekoniecznie jest najmniejszy:

/. 2fcjr . . 2tx\ . .    ,

z» = zo I cos-■ + »sin-1, gazie 1 $ * $ n — 1.

\ n    n /

a)    Zauważmy, że jednym z elementów zbioru ^/(3 —5i)¹ jest liczba zo = 3 - 5i. Drugi element tego zbioru wyraża się zatem wzorem

zi = zo (cos ir + isinnj = (3—5i) •(—!) = —3 + 5i.

b)    Zauważmy, że jednym z elementów zbioru (/(I + i)⁶ jest liczba zo = (1 + «j^a = 2i. Pozostałe elementy tego zbioru wyrażają się wzorem

/ 2kir , . , 2kir\ ...    , _

z* = zo (cos -j- + talu -j-J , gdzie * = 1,2.