IM0

Wzory skróconego mnożenia:

(a+b)²=a²+2ab+b²

(a-b^=a²-2ab+b²

a²-b²=(a-b)(a+b)

(a+b)³=a³+3a²b+3ab²+b³

(a-b^=a³-3a²b+3ab²-b³

a³+b³=(a+b)(a²-ab+b²)

a^b^fa-bjfsP+ab+b²)

(a+b+c)²=a²+b²+c²+2ab+2ac+2bc

Działania na potęgach

a¹=a {a^fi} a-ⁿ=1/aⁿ

gm/n = J^giii gm*gn —gm+n

(a*b)^m=a^m*b^m

(a^m)ⁿ=a^m*ⁿ

a°=1 {a*Q} a"⁴"¹ = aⁿ*a

(a/b)-ⁿ = (b/a)ⁿ {a*M}

_a-(mtn)=V^

a^m/aⁿ=a^m-ⁿ

(a/b)^m=a^m/b^m

Działania na pierwiastkach:

=b { a > 0, b> 0, ne N \ {0,1} }

\/a =-'sflij    \/a *b = \/a *-Vb

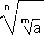
= ⁿ\/a    (Va )^m = tfa™

a*\/b =^aⁿ b    -\/a7b ='s/a / Vb {dla b>0}

(Va)ⁿ=a    \/>£ =/x/    =x

Logarytmy: log_ab=c o a-=b

log_al =0 a^l09_a^b=b

loga(bi*b₂)=log_abi +log_ab₂

log_ab^m=rn*log_ab

log_ab=log_cb/log_ca

{    a€R⁺\ {1} i b<=R⁺    }

log_aa=1

log_b=c oiO^c=b log_abi/b₂=log_ab₁-log_ab₂ log_aⁿVb=1/n log_ab log_ab=1/log_ba

Cechy podzielności liczb naturalnych:

Liczba naturalna jest podzielna przez:
2	qdy jej ostatnią cyfrą jest 0,2,4,6 lub 8
3	qdy suma jej cyfr dzieli się przez 3
4	gdy dwie ostatnie jej cyfry dzielą się przez 4
5	qdy jej ostatnią cyfrą jest 0 lub 5
6	qdy dzieli się przez 2 i przez 3
7	gdy różnica między liczbą wyrażoną kolejnymi trzema ostatnimi cyframi danej liczby a liczbą wyrażoną pozostałymi cyframi tej liczby (lub odwrotnie) dzieli się przez 7
8	gdy liczba, wyrażona trzema ostatnimi jej cyframi dzieli się przez 8
9	qdy suma jej cyfr dzieli się przez 9
10	qdy ostatnią jej cyfrą jest 0
11	gdy różnica sumy jej cyfr stojących na miejscach parzystych i nieparzystych dzieli się przez 11