Image211

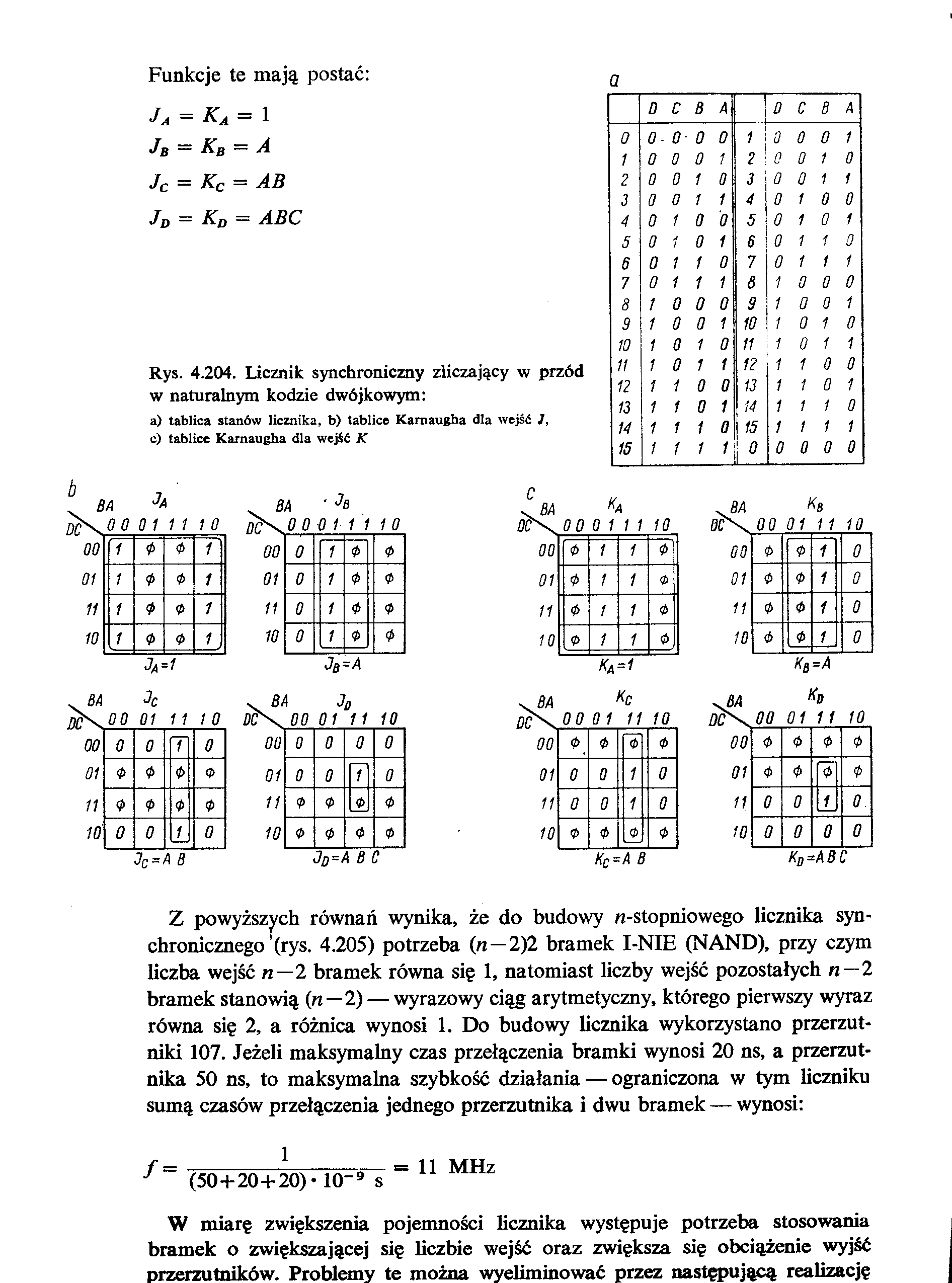
Funkcje te mają postać:

	D	c	8	A		D	c	8	A
0	0-	o•	0	0	1	0	0	0	1
1	0	0	0	1	2 ^!	n	0	1	0
2	0	0	1	0	3	0	0	1	1
3	0	0	1	1	4	0	1	0	0
4	0	1	0	0	5	0	1	0	1
5	0	1	0	1	6	0	1	1	0
6	0	1	1	0	7	0	1	1	1
7	0	1	1	1	8 ^1	1	0	0	0
8	1	0	0	0	^9	\1	0	0	1
9	1	0	0	1	10	I /	0	1	0
10	1	0	1	0	11	1	0	1	1
11	1	0	1	1	12	1	1	0	8
12	1	1	0	0	13	1	1	0	1
13	1	1	0	1	I	1	1	1	0
14	1	1	1	0	I ^15	1	1	1	1
15	1	1	1	1	^0	0	0	0	0

Ja = K_a = 1 J_B = K_B = A J_c = K_c = AB J_D = K_d = ABC

Rys. 4.204. Licznik synchroniczny zliczający w przód w naturalnym kodzie dwójkowym:

a) tablica stanów licznika, b) tablice Kamaugha dla wejść J, c) tablice Karnaugha dla wejść K

^BA Dt^^00		J/ 0 1	I 1 1	1 0	BA ' ^JB r\D00111				1 0	c ^BA	X, 00 0 1		\ 11	10	^8A	00	Kb 01 11		10
00	1	0	0	1'	00	0	1	0	0	00	' 0	1	1	0	00	0	0	1	0
01	1	0	0	1	01	0	1	0	0	01	0	1	1	0	01	0	0	1	0
11	1	0	0	1	11	0	1	0	0	11	0	1	1	0	11	0	0	1	0
10	1	0	0	1 ]	10	0	1	0	0	10	0	1	1	0i	10	0	0	1	0
		JA-	:1				A					Ka-	=1				Kb	=A
	00	Jc 01	1 1	10	v BA 3q /hN. oo 01 11				10	^BA DC\.	Kc 00 0 1 11			10	^BA	00	Kb 01 11		10
00	0	0	T	0	00	0	0	0	0	00	^0.	0	*0	0	00	0	0	0	0
01	0	0	0	0	01	0	0	T	0	01	0	0	1	0	01	0	0	~0	0
11	0	0	0	0	11	0	0	_0	0	11	0	0	1	0	11	0	0		0.
1(3	0	0	]_	0	10	0	0	0	0	10	0	0		0	10	0	0	0	0

0'c*A 8

J_d=A 8 C

Kq-A 8

K_d=ABC

Z powyższych równań wynika, że do budowy n-stopniowego licznika synchronicznego (rys. 4.205) potrzeba (n—2)2 bramek I-NIE (NAND), przy czym liczba wejść n—2 bramek równa się 1, natomiast liczby wejść pozostałych n—2 bramek stanowią (n—2) — wyrazowy ciąg arytmetyczny, którego pierwszy wyraz równa się 2, a różnica wynosi 1. Do budowy licznika wykorzystano przerzut-niki 107. Jeżeli maksymalny czas przełączenia bramki wynosi 20 ns, a przerzut-nika 50 ns, to maksymalna szybkość działania — ograniczona w tym liczniku sumą czasów przełączenia jednego przerzutnika i dwu bramek — wynosi:

/ =

1

(50+20+20)* 10"⁹ s

= 11 MHz

W miarę zwiększenia pojemności licznika występuje potrzeba stosowania bramek o zwiększającej się liczbie wejść oraz zwiększa się obciążenie wyjść przerzutników. Problemy te można wyeliminować przez następującą realizację