img019

bezwzględnej pochodny oraz normalizuje rozkłady skośne ujemnie. Przekształcenie to nie jest tak często stasowane, jak przekształcenia omawiane poprzednio.

2.3.3 Przekształcenie odwrotnościowe

Przekształcenie odwrotnościowe należy również do grupy przekształceń potęgowych. Jest ono określone wzorem:

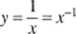
Przekształcenie to stabilizuje wariancję, gdy jest ona proporcjonalna do czwartej potęgi średniej. Jednakże inna cecha lego przekształcenia powoduje, że jest ono często stosowane. Chodzi mianowicie o to, że dużym wartościom ,v przypisuje ono praktycznie zerowe wartości przekształcone, zaś niewielkim wartościom x odpowiadają stosunkowo duże wartości y. Przekształcenie takie ułatwia analizę danych w postaci czasów przeżycia zwierząt doświadczalnych uzyskiwanych np. podczas badań efektywności leków. Zastosowanie tego przekształcenia umożliwia linearyzację spotykanych w tym postępowaniu zależności. Szczegóły omówiono w poniższym przykładzie.

Przykład 2.2

Dla porównania efektu terapeutycznego dwóch leków, zakażono dwie grupy zwierząt doświadczalnych tysiąckrotną „pięćdziesięcioprocentowa dawką śmiertelną" pewnego wirusa. Sposób ustalania pięćdziesięcioprocentowej dawki śmiertelnej, czyli takiego stężenia wirusa, przy którym połowa zwierząt doświadczalnych ginie, będzie opisany w następnym podrozdziale. Teraz zakażone zwierzęta leczono badanymi lekami podając jednej grupie jeden z leków, a drugiej — drugi. W ramach każdej z grup aplikowano poszczególnym zwierzętom różne dawki, a właściwie różne stężenia odpowiedniego leku. Rejestrowano czasy przeżycia poszczególnych zwierząt, rodzaj podawaitego im leku oraz jego stężenie podczas terapii. Następnie tak uzyskane dane poddawano przekształceniom wykorzystując logarytmy stężenia leków (log D) oraz odwrotności czasów przeżycia (1/7). Przekształcone dane naniesiono na układ współrzędnych o osiach log D oraz 1/T (patrz rys. 2.2). Dalsze badania statystyczne wykazały, że z dostatecznie dużym prawdopodobieństwem można:

1)    zależności między 1/7' a log D dla każdego z dwóch badanych leków traktować jako prostoliniowe o współczynnikach kierunkowych prostych różnych od zera (por. podrozdział 8.3),

2)    obie proste obrazujące te zależności uważać za równoległe (por. punkt 8.4.1),

3)    traktować równoległe proste dla obu leków jako proste nic pokrywające się i oszacować ich poziomą odległość M (por. punkty 8.4.3. 8.4.5. a także rys. 2.2).

19