img027

układu (rys. 15). Ha rysunku układ orientujsrny zwykła w tan sposób, aby fcicrunok dodatni osi z był zwrócony ku górze arkusza.

Kąty liczona w prawo, zgodni* z ruchem wskazówki zegara, od dodatniego kierunku osi x do poszczególnych kierunków są azymutami kartograficznymi ct_fc. Układ geodezyjny y x bywu również nazywany układem prawoskręt-aya,

Fołożenie punktu P (y, x) na płaszczyźnie poziomej określają dwie współrzędna: 7 (rzędna) i x (odcięta). Współrzędne y i m są to odległości od początku układu 0 do rzutu punktu P na oś y i na oś r. Powyżej określone współrzędne prostokątne są nazywane flapćłrzędnyai prostoliniowymi lub kartczjańckimi.

Oaie układu współrzędnych dzielą płaszczyznę as cztery ćwiartki, które oznaczany kolejnymi numerami (cyframi rzymskimi) lub według stron świata, jak na rysunku 15. Znaki współrzędnych 7 i z w poszczególnych ćwiartkach są następujące:

Ćwiartka	Znaki y	Znaki z
I (NO)	+	♦
II (SO)	♦	+
III (ÓS)	-	-
IV (KI)	-	+

T celu ułatwienia obliczeń obieramy zwykle początek układu współrzędnych w tan sposób, aby rzędne 7 i odcięte z wszystkich punktów opracowywanego obszaru były dodatnie.

N

9	"^x m
MW	MO
*y &	L -a
P^[JŁ
t	IV
sir	+x SO

S

Rys. 17

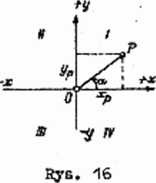
Jak widzimy, geodezyjny układ różni się od ma te ma tycznego (rys. 16) kierunkiem osi y i x, gdyż w układzie matematycznym kierunek dodatni ęsi z sprowadzamy do dodatniego kierunku osi y przez obrót w lewo o 90°, a kąty kierunkowe a. liczymy od dodatniego kierunku osi x w lewo (układ 1«-wcsfcrętny). Oznaczenia ćwiartek układu matematycznego przyjmujemy jak na rysunku Ib. Z porównania układu geodezyjnego (rys. 15/ i automatycznego (rys. 16) znaków x i y « każdej ćwiartce oraz wartości kątów kierunkowych liczonych dla kierunków wychodzących 2 początku układu, widzimy żc wzory matematyczne ais układu matematycznego osi współrzędnych asją zastosowanie bez zmiac rówaiaż dla układu geodezyjnego-