img067

67

6.2. Problem wyboru funkcji bazowych

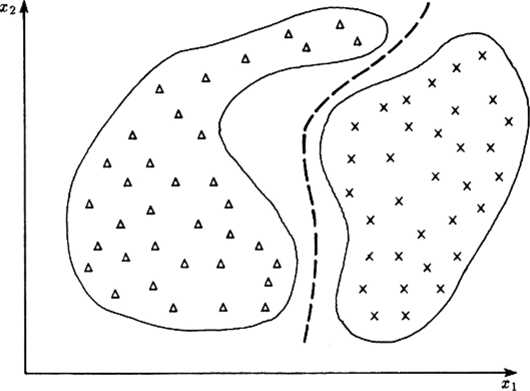
Rys. 6.1. Mato skomplikowanym kształtom obszarów obrazów w przestrzeni cech odpowiadają gładkie powierzchnie rozgraniczające te obszary

Postulaty pod adresem rodziny funkcji $ można więc zebrać w następującej postaci: ma to być rodzina ortonorinalnych funkcji n zmiennych o wzrastającej dziwaczności. Rodzinę taką można utworzyć na podstawie łatwo dostępnej rodziny funkcji jednej zmiennej o tych samych własnościach. Niech /„(z) (fi = 0,1,2, ...) będzie rodziną ortonormalnych funkcji jednej zmiennej o rosnącej dziwaczności. Wówczas można budować rodzinę <J>, korzystając z formuły kanonicznej

n

w(x)=n fuM*)'    (⁵ⁱ)

i?=i

w której spełniony musi być warunek

n

(52)

= v.

n=i