img079

79

6.5. Metoda funkcji nieliniowych

(rys. 6.6), pochodzące od ciągłych obrotów płaszczyzny granicznej, wymuszanych błędnymi rozpoznaniami (rys. 6.7).

6.5. Metoda funkcji nieliniowych

Możemy teraz wrócić do ogólnego sformułowania zadania (wzór (47)). Jakie zalety może mieć zastosowanie ogólnej formuły (47) w stosunku do wzoru dla funkcji liniowych (58)? Otóż wydaje się, że można wskazać przynajmniej dwa powody, dla których użycie formuły (47) może przynieść sukces w warunkach, kiedy wzór (58) nie doprowadził do zadowalających wyników:

1.    Stosując wzór (47), możemy generować w przestrzeni cech powierzchnie rozgraniczające o dowolnych kształtach (por. (50)), a nie tylko hiper-płaszczyzny. Pozwala to na rozgraniczenie obszarów liniowo nieseparowal-nych. Już tylko zastosowanie we wzorze (47) wielomianów drugiego stopnia pozwala uzyskiwać jako powierzchnie separujące: elipsoidy, paraboloidy, hiperboloidy oraz ich dowolne kombinacje.

2.    Stosując wzór (47), mamy do dyspozycji m dobieranych współczynników, przy czym na ogół m > (n+ 1). Istnieje zaś twierdzenie pokazujące związek pomiędzy liczbą nastawialnych wag a prawdopodobieństwem poprawnego rozpoznawania (por. [7]), przy czym wniosek z tego twierdzenia wskazuje na celowość zwiększania m w przypadku trudności z rozpoznawaniem.

Tak więc celowe jest przyjęcie metody rozpoznawania opartej na funkcji przynależności postaci:

m

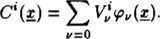
(69)

Jak w przypadku takiej funkcji prowadzić proces uczenia, to znaczy znajdowania wag V' ? Otóż łatwo wykazać, że skuteczny jest ponownie algorytm dany wzorami (66) i (67) pod warunkiem odmiennego zinterpretowania zmodyfikowanej zmiennej x. Załóżmy, że związek pomiędzy wektorem cech x a wektorem zmodyfikowanym i jest dany nie wzorem (63), lecz zależnością:

(70)

x„ = f>_v(x)\ i/ = 0,1.....m.