img345

średniej p tej zmiennej wektorem średnich (i i wreszcie wariancji o² — macierzą kowariancji zmiennych X\, x_p.

Funkcja gęstości prawdopodobieństwa ma wówczas rozkład dany wzorem

(5)

^Ax)= (lny'²nr^cxp “2^{(a:_m)7S (}-^v_^

Na podstawie tej funkcji gęstości stwierdzamy, że punkty x o jednakowej gęstości prawdopodobieństwa leżą na powierzchni elipsoidy w /^-wymiarowej przestrzeni o równaniu

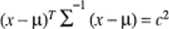
(6)

Elipsoida ta nazywa się elipsoidą koncentracji i stanowi uogólnienie granic (p - cc), (p + ro) obszaru rozproszenia jednowymiarowej zmiennej losowej o rozkładzie normalnym.

Identycznie jak poprzednio, rozkład normalny wielowymiarowej zmiennej losowej x notujemy jak poniżej:

(7)

.t = N(p,£>

Rozkład normalny wielowymiarowy jest jednoznacznie określony, gdy dane są średnie wszystkich zmiennych oraz ich wariancje i kowariancje.

Przytoczymy jeszcze dwa ważne twierdzenia:

• TW l. Jeżeli /^-wymiarowa zmienna losowa x ma rozkład A/(p. Z) i jeżeli U jest macierzą typu (p, u) rzędu //, to wówczas w-wymiarowa zmienna losowa

ma rozkład normalny N(U^TH,U^TlU) .

• TW 2. Jeżeli />-wymiarowa zmienna losowa x ma rozkład /V(p, Z) gdzie Z jest macierzą kowariancji a IZI oznacza wyznacznik tej macierzy, to prawdopodobieństwo, że między składowymi wektora x zachodzi przynajmniej jeden związek liniowy, jest równe jedności wtedy i tylko wtedy, gdy

IZI = 0 .

345