KINEMATYKA0029

RZUTY

( Nie jest to takie trudne !!!

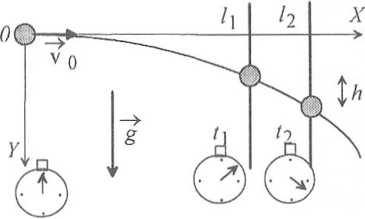
Ten skomplikowany ruch rozpatruje jako złożenie jednostajnego ruchu poziomego i jednostajnie przyspieszonego ruchu l pionowego

Wybierzmy układ współrzędnych jak na rysunku (jego początek w miejscu wystrzelenia kuli). Ponieważ wektor przyspieszenia g jest skierowany pionowo, ruch poziomy jest ruchem jednostajnym. Zatem równanie ruchu dla składowej x ma następującą postać (patrz wzór (1.14)):

X =V()',

gdyż w chwili początkowej przyjmujemy x = 0. Pocisk dolatuje do kartek w chwilach i\ \ h (/| < 12). W tych chwilach powyższe równanie ruchu przechodzi w równania:

/1 =V()/|, 12 =V2-

W równaniach tych występuje szukana wielkość v₍₎, ale również nieznane wielkości: i\ i /₂-Wyraźmy czasy t\ i /₂ przez v₍₎ :

>\ >2 ^,l'vo’^,2    v₀-

Rozpatrzmy teraz ruch pionowy. Jest to ruch jednostajnie przyspieszony, zatem równanie ruchu dla składowej Y zgodnie z zależnością (1.17), po uwzględnieniu wybranej osi i jej kierunku, ma postać:

Oznaczając przez y\ i y-> współrzędne położeń punktów, w których pocisk przebił kolejno obie kartki, możemy zapisać powyższe równanie dla chwil /1 i /₂ :

12 12

yyi = p^l2-

W treści zadania nie mamy jednak danych wartości y\ i y₂ , znamy za to wartość h, która zdefiniowana jest jako: h - j'₂ -jj. W ostatnim równaniu podstawimy otrzymane wyrażenia na y\ i y₂ :

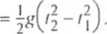
^{h =} h'^/22-Wi

Rozpatrując ruch wzdłuż osi ()X, wyraziliśmy czasy i \ \ przez v₍₎. Skorzystajmy teraz z tego przekształcając dalej ostatnie równanie:

(£)²-fe)²l =

Z tej zależności wyznaczymy szukaną prędkość początkową (wszystkie pozostałe wielkości znamy). Mamy:

36