Mechanika ogolna0041

X2

X2

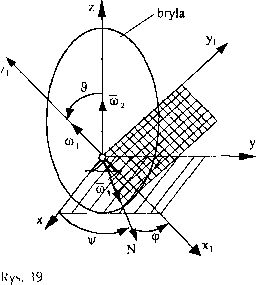
Oxyz - nieruchomy uldad odniesienia x₁yiZ₁ - ruchomy układ odniesienia związany z bryłą

N - tzw. linia węzłów (krawędź przecięcia płaszczyzny xy z płaszczyzną x_tyi)

Zgodnie z rys. 39 ruchy wektora chwilowej prędkości kątowej na odpowiednie osie będą następujące:

(145)

co_X) = Ś"COS(p-\j/-sin9 co_y[ =-^-sin(p + vj/-cos(p co_Zi = (p + vj/ • cos $

Uproszczona teoria ruchu kulistego

Zbadamy szczególny przypadek ruchu kulistego. Załóżmy, że bryła ma oś symetrii, i że środek ruchu kulistego O leży na tej osi. Elipsoida bezwładności liikiego ciała w punkcie O jest elipsoidą obrotową. Oś symetrii i każda oś do niej prostopadła są głównymi osiami bezwładności ciała w punkcie O. Załóżmy, że eialo wykonuje specjalny rodzaj ruchu polegający na tym, że obraca się wokół osi symetrii ze stałą co do wartości prędkością kątową ©!, a jednocześnie oś la obraca się wokół innej osi nieruchomej przecinającej się z osią obrotu własnego w punkcie O, ze stałą prędkością kątową ©2. Ruch taki nazywa się prece-•.I;| regularną. Zbadamy, jakie siły należy przyłożyć do ciała, aby utrzymać go w takim ruchu.

Przyjmijmy początek układu ruchomego i nieruchomego w środku ruchu kulistego O (rys. 40). Oś z układu nieruchomego skierujemy wzdłuż weklora au. < )ś /| układu ruchomego wzdłuż osi symetrii, a jednocześnie oni obrotu własnego, czyli zgodnie z wektorem (o,. Wektor wypadkowy prędkości kątowej jest /.łożeniem geometrycznym prędkości kątowej obrotu własnego i prędkości kątowej precesji <b₂. Mamy więc:

(146)

coj = <p = const. 1 co₂ = y = const. co₃ =0    j

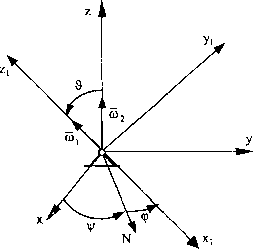
Rys. 40

Równania (146) opisują prędkość kątową ruchu kulistego. Ponieważ co₃ =0 (piędkość kątowa nutacji), to mówimy, że ruch taki jest precesją regularną. Jeżeli co, »co₂, to można przyjąć, że:

K_w =K_Zi = I_Zi - co,    (147)

udzie l_z - moment bezwładności bryły względem osi obrotu własnego.

h/yjmujemy więc, że kręt rozpatrywanego ciała leży na osi obrotu i jego wartość nie zależy od CO2:

(148)

K „ = K_Z = I_z • «>! = const.

/miana krętu wywołana jest więc tylko obrotem wektora krętu razem z osią z_x wokół nieruchomej osi obrolu z. Zmianę (ę zapiszemy w postaci:

(149)