Mechanika ogolna0063

126

Zależność (193) nazywamy zasadą zachowania energii mechanicznej (lub całkowitej):

H - energia mechaniczna w położeniu I,

Hu - energia mechaniczna w położeniu II.

Uwaga!

Potencjał układu jest sumą algebraiczną potencjałów pochodzących od poszczególnych pól potencjalnych.    *'

Przykład 17

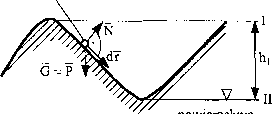
Punkt materialny porusza się w polu ziemskim po trajektorii pokazanej na rys. 73. Zakładamy zerowe warunki początkowe. Określić, jaką prędkość będzie miał punkt w położeniu II. Opory ruchu pominąć.

m

powierzchnia

porównawcza Rys. 73

Oznaczmy przez P siłę pola potencjalnego ziemskiego działającą na punkt małe rialny. Zgodnie z założeniami punkt startuje z położenia I z zerową prędkośei;| Przyjmujemy poziom porównawczy w położeniu n. Odległość od poziomu I do poziomu II wynosi hi. Oprócz siły pola potencjalnego na punkt działa reakcja podłoża N, która nie wykonuje pracy, gdyż jest prostopadła do wektora cle mentamego przesunięcia dr. W naszym układzie pracę wykonuje tylko siła pola potencjalnego, więc z zależności (193) będziemy mieli:

Hj = Ej + Vj - energia mechaniczna położenia I,

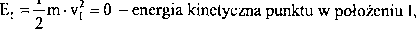
V, =m’g-h, - potencjał w położeniu I określony względem poziomu po

równawczego.

Energia mechaniczna w położeniu I wynosi więc: Hj = m • g • h,.

W odniesieniu do położenia II mamy:

^En = 2^m'^Vii

- energia kinetyczna w położeniu II,

V_n = 0 - ponieważ w położeniu II przyjęliśmy poziom porównawczy, energia mechaniczna w położeniu II wynosi:

^Ha =^m-Vn-

Z zasady równowagi energii mechanicznej punktu mamy:

,1 2

m-g-łi! = —m-v_n,

stąd otrzymujemy prędkość punktu w położeniu II, która wynosi: v„ = yj2-g-hj.

Przykład 18

Opisać ruch wahadła fizycznego (rys. 74). Wahadło zostało wychylone o kąt cp do położenia oznaczonego I i następnie puszczone swobodnie. Mamy określić prędkość kątową bryły w momencie, gdy znajdować się będzie w położeniu II.

Ryn. 74

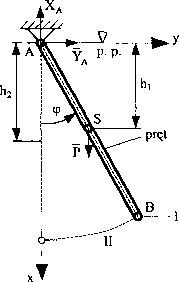
Dane:

P - siła ciężkości pręta (wahadła) [N], AB = l - długość pręta [m].