Mechanika ogolna0077

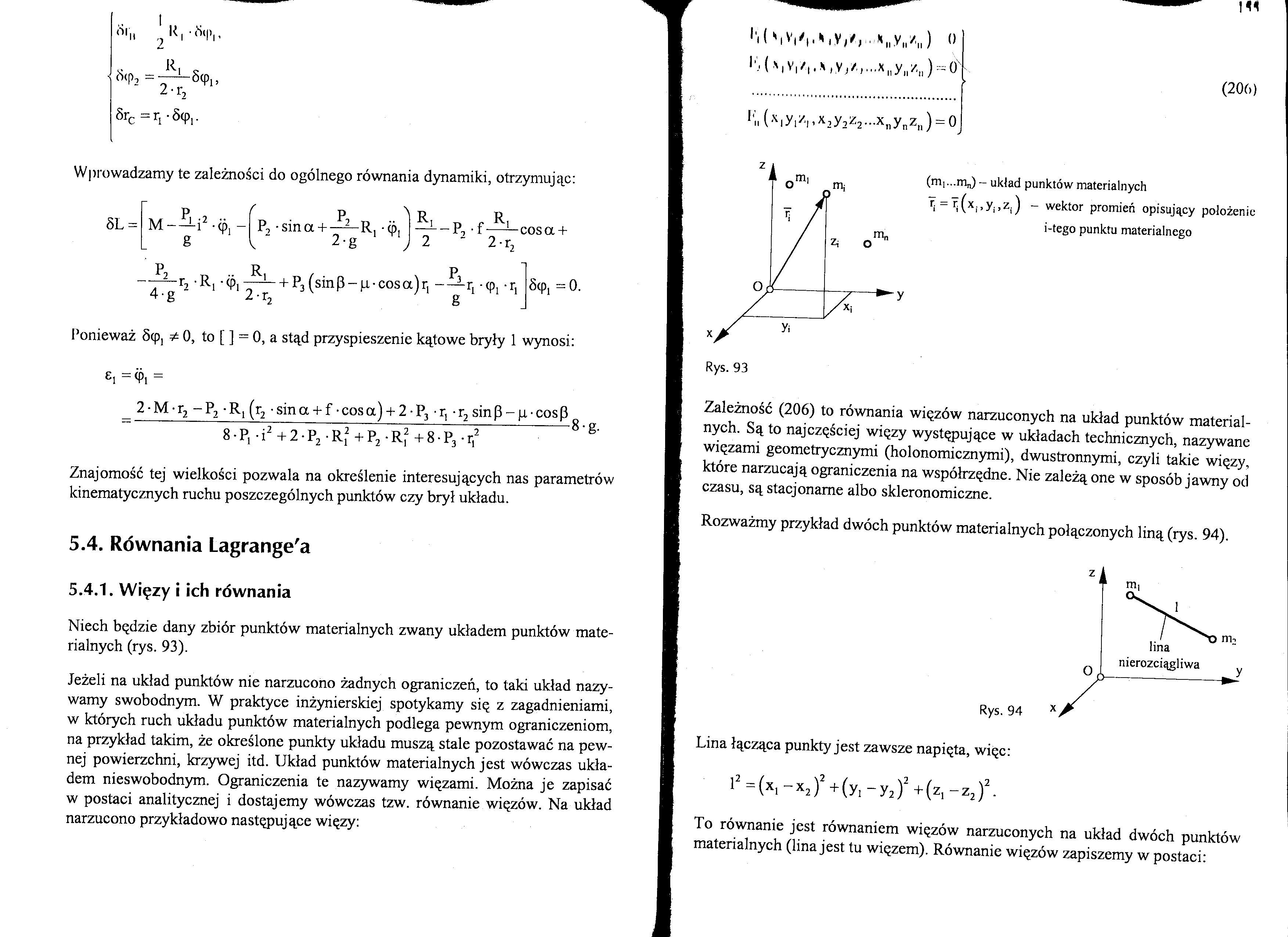
<S||,    ^K, •««!>,,

. R, ,

&‘P₂

2-r,

8r_c = r, • 8(p,.

—i²'<Pi g

n . p, „	.. j R,	-P,-f
- P, -sina-f——R, l ‘ 2-g	%)-
^ + P3(smP-u-	cosa)r,	-V
2 -r2 ^v		g

A.

2-r,

Wprowadzamy te zależności do ogólnego równania dynamiki, otrzymując: 8L =

4'g

8cp, =0.

Ponieważ Sep, =£ 0, to [ ] = 0, a stąd przyspieszenie kątowe bryły 1 wynosi:

^el^=<Pl =

8-g.

_ 2-M-r₂ -P, -R,(r₂ -sina + f-cosa) + 2-P₃ r, -r₂sinp-p-cosP 8 • P, • i² + 2 • P, • R? + P, • R? + 8 • P, • r,²

Znajomość tej wielkości pozwala na określenie interesujących nas parametrów kinematycznych ruchu poszczególnych punktów czy brył układu.

5.4. Równania Lagrange'a

5.4.1. Więzy i ich równania

Niech będzie dany zbiór punktów materialnych zwany układem punktów materialnych (rys. 93).

Jeżeli na układ punktów nie narzucono żadnych ograniczeń, to taki układ nazywamy swobodnym. W praktyce inżynierskiej spotykamy się z zagadnieniami, w których ruch układu punktów materialnych podlega pewnym ograniczeniom, na przykład takim, że określone punkty układu muszą stale pozostawać na pewnej powierzchni, krzywej itd. Układ punktów materialnych jest wówczas układem nieswobodnym. Ograniczenia te nazywamy więzami. Można je zapisać w postaci analitycznej i dostajemy wówczas tzw. równanie więzów. Na układ narzucono przykładowo następujące więzy:

^1,n(^Xiy.^Zl^2y2^Z2-^X„ynZ₁₁) = 0

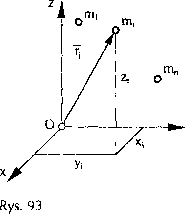
(m₁...m„) - układ punktów materialnych r = r^j.y.,z_t) - wektor promień opisujący położenie i-tego punktu materialnego

Zależność (206) to równania więzów narzuconych na układ punktów materialnych. Są to najczęściej więzy występujące w układach technicznych, nazywane więzami geometrycznymi (holonomicznymi), dwustronnymi, czyłi takie więzy, które narzucają ograniczenia na współrzędne. Nie zależą one w sposób jawny od czasu, są stacjonarne albo skleronomiczne.

Rozważmy przykład dwóch punktów materialnych połączonych liną (rys. 94).

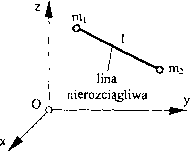
Rys. 94

Lina łącząca punkty jest zawsze napięta, więc: l² = (x, - x₂ )² + (y, - y₂ )² + (z, - z₂ )².

To równanie jest równaniem więzów narzuconych na układ dwóch punktów materialnych (lina jest tu więzem). Równanie więzów zapiszemy w postaci: