Mechanika ogolna0037

74

ożyli:

1:

Ri '<Pi -2-y_B = 2-r₂ -q>₂, q -<p, = u_c.

Różniczkując powyższe wyrażenia, otrzymamy zależności kinematyczne na przyspieszenia:

1

Ri '9i =2-y_B=2-r₂-(p₂

ą-ćp, =ii_c.

Układ równań (10) to zależności wynikające z kinematyki układu. Określimy momenty bezwładności brył. Dla bryły 1:

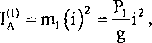
dla bryły 2:

Rozwiązujemy poszczególne równania w następującej kolejności:

• z równania (2) mamy X _A = N ₃ • cos a,

• z równania (3) mamy Y_A = P; + N₂ + N₃ • sin a,

•    z równania (8) mamy N = P₃ • cos a.

Idy la 1 jest w ruchu postępowym. Siła tarcia jest równa tarciu rozwiniętemu, ożyli:

T = p- N = p-P₃ cosa.

P, ₂

g

P

zo wzoru (5) mamy — y_B = N₂ + N₄ -P₂, g

/o wzoru (1) mamy —i -ip, =M + N₃-r,-N₂-R,,

Jr/cli np. interesuje nas kinematyka bryły 1, to rozwiązanie prowadzimy w na-ttlępujący sposób:

/ tównania (7), uwzględniając (10), dostaniemy:

\\

•—r, - ćp, = P₃ (sin a - p ■ cos a) - N₃.

g

/ i ównania tego wyznaczymy reakcję N₃:

p

N₃ = P₃ (sin a - p • cos a)—-r, -ćp,.

g

/ ińwnań (5) i (10) wynika, że: g 2

Mipl reakcja N₄ będzie następująca:

N₄ ⁼^2 ^—N₂ +— Rj ■ <Pj.

2-g

Hównanie (6), po uwzględnieniu zależności (10) oraz wartości N₄, zapiszemy w poslaci:

=N₂ -p₂ +n₂-JLr,-ćp,,

2-g    2 -r₂    2-g

p- r/rgo wyznaczymy reakcję N₂:

P    3 P

2    8 g

Wim nmy do pierwszego równania. Za wszystkie reakcje wstawiamy wyznaczona wielkości. Dostaniemy wówczas:

2

P    P    3 P

r -ip, =M + P₃ -r^sina-p-cosa)-—r² -ćp, —-R₃---^ŁR² -ćp..

g    2    8 g l'i /.yupicszenie kątowe bryły 1 będzie więc wynosić:

•Pi

2-M + 2-P, -r,(sina-Li-cosa)-P, -R. _ ------------------ • 4 • g.

8 • P, - i² -ł- 3 ■ l», ■ !</ I 8-1’, -if l*o Meiilkownniu określimy <p, om/ qt|