Mechanika ogolna0037

74

czyli:

|Ri '91 ~2-y_B =2-r₂ -<j>_2}

Vr«p,=u_c.

Różniczkując powyższe wyrażenia, otrzymamy zależności kinematyczne na przyspieszenia:

£

S-i '9i ~ 2-y_B =2-r₂ - ip₂ r_r(p, =ii_c.

Układ równań (10) to zależności wynikające z kinematyki układu. Określimy momenty bezwładności brył. Dla bryły 1:

g

dla bryły 2:

Rozwiązujemy poszczególne równania w następującej kolejności:

•    z równania (2) mamy X _A = N ₃ • cos a,

•    z równania (3) mamy Y_A = P, + N₂ + N₃ • sin a,

•    z równania (8) mamy N = P₃ • cos a.

Bryla 1 jest w ruchu postępowym. Siła tarcia jest równa tarciu rozwiniętemu, czyli:

T = p-N = p-P₃ cosa.

p, -

g

P

/.o wzoru (5) mamy — y_B = N₂ + N₄ -P₂,

Ze wzoru (1) mamy —i • <p, = M + N₃ • ^ - N₂ • R,,

g

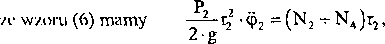
—ii₍. ~ P, • sin a - p • P, • cos a - N,.

g

zo wzoru (7) mamy

,1 rżeli np. interesuje nas kinematyka bryły 1, to rozwiązanie prowadzimy w na-Mltjpiijący sposób:

/ równania (7), uwzględniając (10), dostaniemy:

p

--- r, - cp, = P₃ (sin a - p • cos a) - N₃. g

f równania tego wyznaczymy reakcję N₃:

p

N₃-P₃(sina-p-cosa)—— r₃ -ćp,.

g

/ ińwnań (5) i (10) wynika, że:

'LJkjp ^

g 2

hlii<I reakcja N₄ będzie następująca:

N₄ ⁼^2 ^— N_z +    ² R-i ^-9i-

2-g

llównanie (6), po uwzględnieniu zależności (10) oraz wartości N₄, zapiszemy

w postaci:

^Ri

2-g    2-r,

2-g

^Rr<Pi,

f r/rgo wyznaczymy reakcję N₂:

Wmi iiiny do pierwszego równania. Za wszystkie reakcje wstawiamy wyznaczona wielkości. Dostaniemy wówczas:

I * ■ > ..    , , _D    3 Pj j .. Pj_    3 P, ₂ ••

i' -(p, =M + P₃ -r,(sina- p-cosa) —-r, -ćp, —-R,----Rf ■ cp,.

W    -    g    2    8 g

['i /yspieszonie kątowe bryły 1 będzie więc wynosić:

'l'i

2-M + 2-P₃ - r^sina-p-cosaj-P, -R,

8 • P, - i² -ł- 3 ■ l», ■ R j' i 8-1’, -if

■4-g.

|'o Mt-nlkownniii określimy tp, om/<|>i