P5194054

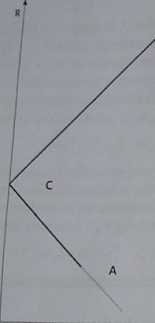
Wykres 6.3

Współczynnik korelacji=-1

taotlon of ihe efficienl pet j p/nber 1972.

Por. n§! Por. nttj

Źródło: Opracowanie własne.

Punkty A i B oznaczają portfele złożone wyłącznie odpowiednio z papieraJ wartościowych A lub B, zaś linie przerywane utożsamiają krótką sprzedaż- przykU dowo, biorąc pod uwagę wykres 6.3 - linia przerywana poniżej punktu A oznacza krótką sprzedaż papieru wartościowego B i nabycie dodatkowych walorów B. Godna zauważenia jest możliwość konstrukcji portfela bez ryzyka w przypadku, gdy współ| czynnik korelacji wynosi -1 (portfel został odzwierciedlony przez punkt C).    i

Wyznaczenie zbioru efektywnego (zestawu portfeli optymalnych z punktu roi dzenia kombinacji stopy zwrotu oraz ryzyka) jest możliwe przy uwzględnienĘwsiftj kich wartości współczynnika korelacji oprócz skrajnej 1 Gdy współczynnikiorelag] jest równy 1, inwestor dokonuje wyboru „coś za coś” (ang. trade ofj), albowiemnienuj takiej sytuacji, że dany portfel jest obiektywnie lepszy od innego (generuje wyższąslo-j pę zwrotu przy danym poziomie odchylenia standardowego lub przy dang stopief zwrotu odznacza się niższym ryzykiem). Ilustracją przypadku jest wykres 6.1.    f

Gdy współczynnik korelacji jest równy -1 granica efektywna przyjmuj!postać! pólprostej o nachyleniu dodatnim zgodnie z wykresem 6.3. W pozostałych pCzypad-l kach granicy efektywnej odpowiada górna połowa hiperboli równoosiowej^H

Fakt ten został zauważony przez R. Merlona. Por. Merton R.: Am folio frónttm, Journal of Financial and Quantitive Analysis”A

p Wieloelementowy portfel akcyjny

Łstosowanie w praktyce teorii portfela dwuelementowego w dobie globalizacji Klizacji rynków finansowych jest ograniczone - inwestor posiada zazwyczaj K] ^elu papierów wartościowych, zróżnicowanych pod względem ryzyka (rów-^ profilu ryzyka), oczekiwanej rentowności, kraju pochodzenia, płynności, praw (ługujących ich właścicielowi i innych cech.

[Oczekiwana stopa zwrotu portfela wieloelementowego, podobnie jak miało to |lejsce dla portfela dwuelementowego, jest równa średniej ważonej oczekiwanych Kwności akcji wchodzących w skład portfela, zgodnie ze wzorem (6.6J⁴:

Rr-^to^R,    (6.6)

-1, (o, *0 dlai=l,2.....n.    (6.7)

|dziew-udział akcji i w portfelu.

Wariancja portfela wieloelementowego opisana została wzorem (6.8)*:

V_P = X sf + J jjOJ, % (Oj *s,*Sj*o_v    (6.8)

■Oy - udziały akcji i oraz j w portfelu,

§w__7 ^odc^y¹enia standardowe stópzwrotu akcji i oraz j,

współczynnik korelacji pomiędzy stopami zwrotu akcji i oraz/', r uwagi na fakt, że o_(J=o,jdrugi składnik prawej strony równania opisanego wzo-1(6.8) nie został pomnożony przez liczbę dwa.

■Odchylenie standardowe portfela wieloelementowego (s_PW) wynosi zgodnie ze porem (6.9):

⁽⁶'⁹⁾

J Zbiór wszystkich portfeli wieloelementowych, które można skonstruować przy lanym poziomie odchyleń standardowych, rentowności oraz współczynników kore-cji zobrazowany został na wykresie 6.4.

Przedstawiona pa wykresie 6.4 figura to zbiór możliwości (ang. opportunity set), Iwana również potocznie „pociskiem Markowitza”. Zbiór możliwości pokazuje Kszystkie możliwe do skonstruowania portfele, jego kształt zależny jest od liczby Wólek branych pod uwagę - liczba spółek determinuje liczbę wierzchołków figury,

[A. R., op. dt., 179.

Jnwestycje, analiza i zarządzanie. WIG Press, Warszawa 2000, s. 261.