Rotacja

i„rotv = rot„v

DOTACJA

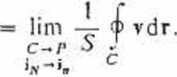
(1.36)

Każdemu punktowi P obszaru przestrzennego R. w którym istnieje pole wektorowe v, możemy w ten sposób przyporządkować nową wielkość wektorową — rotację tego pola rotv. Dowód twierdzenia wyrażonego wzorem (1.36) można znaleźć w podręcznikach analizy wektorowej; w przypisie 1.1 pokazujemy, że w kartezjańskim układzie współrzędnych prostokątnych wektor rotv ma składowe

rot_x v =

rot_yv =

rot. v = czyli rotv = i

***•' W 1/ •	a-
8y	'i- ’ OZ
dvx	8v2
oz	8x ^5
8l'y	8vx
8x	r* J oy
1^dv*	8v.

* \ By oz )

(I.37a)

+ i_y

12i'x	^3M, i i	i *>t	Bvx\
\ 8z	dx)+ ^s'	la*	9y)

V x v.

(I.37b)

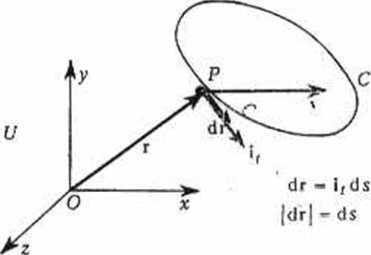
Krążenie (cyrkulacja) wektora pola v wzdłuż krzywej zamkniętej C: całka

krzywoliniowa f vdr.

ć

* Oczywiście przy opisanym przejściu granicznym ściągania krzywej C do punktu P pole powierzchni S rozpiętej na krzywej C dąży do zera: S -* 0.

^— 3.2AF(22EWSKl

T-JL 02,{..

₄₆ wsrępa>o Fi2yv<i