scan#

a₄ = 2-(U5)⁴"¹

a₄ = 2-(U5)³ = 2^-|-j³ =

do wymienionego wzoru podstawiamy dane z zadania

₂ 125 ₌ 125

>r 32

Teraz znajdujemy S„ (sumę n początkowych, kolejnych wyrazów ciągu geometrycznego)

W

tym celu posłużymy się wzorem S_n = a_:

.1^1

\-q

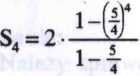
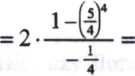
do wymienionego wzoru podstawiamy dane z zadania

— 2 • (-4) • (1 —4^> ⁼

•ts(>

= -8(-

256    625

o/

265

3. -! h

265

) =

256 - 625

32

-369    369

32

32

ę _ 369 ⁴    32

e _ 369 ⁴    32

°^dp* ^a4=~W~

Zad.6.

Wiedząc, że ciąg jest geometryczny i mając dane a_t = 3; n = 5; a_n = 12 znajdź: q, S„.

Rozwiązanie:

Najpierw znajdujemy q (iloraz ciągu geometrycznego).

/I—^fl

W tym celu posłużymy się wzorem a_n = a_{q

stąd

stąd

12 = 3 • q

5-1

3- q^Ą= 12

?⁴ = 4

W²)" = 4

r=2

lub

q² = l

q = -V2 lub

/: 3

do wymienionego wzoru podstawiamy dane z zadania

rozwiązujemy równanie potęgowe korzystając ze wzoru

(<7²)² = <7⁴

q‘ = -2

to równanie nie ma rozwiązania

__

-V2

Teraz znajdujemy S„ (sumę n początkowych wyrazów ciągu)

j_ n

W tym celu posłużymy się wzorem S„ = a_x • ^

Ponieważ uzyskaliśmy dwie wartości ilorazu (- "N\l oraz "N12) sumę obliczamy osobno dla q = -^l2 i osobno dla q = ^l2.

Dla q = -^l2

S_{u = 3}.i^4£ = 3.i^ = ¹²    l-(-V2)    1 + V2

-63 _ -189

1 + V2 1 + V2

= 3-

49