skanowanie0057 (2)

z

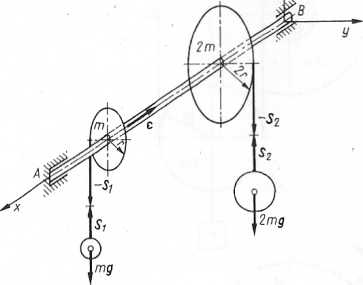
Rys. 6.6. Do przykładu 6.6

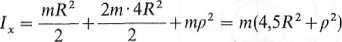
Zatem dynamiczne równanie ruchu obrotowego wału z obydwoma krążkami ma postać (rys. 6.6)

1.    I_xe = 2RS₂-RS₁

Dynamiczne równania ruchu obciążników (rys. 6.6):

2.    meR = S_l—mg

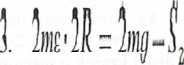
Z otrzymanego układu trzech równań możemy wyznaczyć przyspieszenie

kątowe e

6gR

⁸    27R²+2p² S

-2

Stąd po przyjęciu warunków początkowych: dla t = 0: o)₀ = 0 obliczamy wartość prędkości kątowej

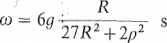
-i

Przykład 6.7. Na wale AB o długości 31 ułożyskowanym w punktach

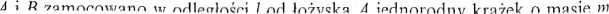
i promieniu R. W odległości / od łożyska B przymocowano do wału pręt CD

0    długości 2R. Osie wału i pręta przecinają się i są do siebie prostopadłe. Na końcach pręta zamocowano kule o promieniach R i masach m tak, że środki kul

1    oś pręta leżą na jednej prostej. Wokół krążka owinięto nierozciągliwy i nieważki sznur, na końcu którego zawieszono i swobodnie puszczono obciążnik o masie m (rys. 6.7). Obliczyć siłę S naciągu sznura podczas opadania obciążnika w dół. Wał AB i pręt CD należy traktować jako nieważkie.

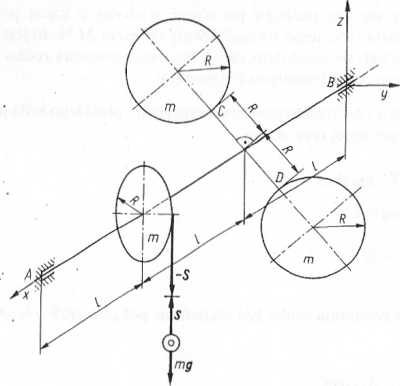
Rys. 6.7. Do przykładu 6.7

ii

jest równy

l_x = 2 j^-j mR²+4mR²j+= 9,3 mR²

Dynamiczne równanie ruchu obrotowego układu (bez obciążnika) wynosi i. I_xs = SR

Dynamiczne równanie ruchu obciążnika (rys. 6.7)

2. meR — mg—S

Stąd

S = —= 0,903mg N mR²

T