skanuj0023

44
3. Obliczamy przyspieszenie ziemskie g ze wzoru (2).
4. Obliczamy maksymalną niepewność względną pomiaru pośredniego g (cz.I p.5.2 wzór (18)):
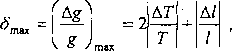
(3)
niepewność procentową:
<$/„ = <wioo%
oraz niepewność maksymalną:
(Ą§)max — g'Sinax •
Wynik naszych obliczeń zapisujemy w postaci:
g± Ag.
4. Następnie oceniamy wkład wniesiony przez niepewności pomiaru poszczególnych wielkości prostych, tj. T i / do niepewności wyznaczania wielkości złożonej, g. W tym celu porównujemy ze sobą oba składniki w sumie (3).
5. Sprawozdanie kończymy wnioskami, w których powinno znaleźć się zestawienie uzyskanych wyników, porównanie uzyskanej wartości przyspieszenia ziemskiego z wartością gtab dla Krakowa podaną w tablicach znajdujących się na końcu skryptu oraz ocena dokładności pomiarów na podstawie p.4.
Zastosowana przez nas metoda pomiarowa opierała się na przybliżonym wzorze (1), który jest słuszny tylko dla małych wychyleń i drgań odbywających się w jednej płaszczyźnie. Jeśli tego nie dopilnujemy w trakcie pomiarów, pojawią się błędy wpływające na końcowy wynik.
Należy również zdać sobie sprawę z tego, że otrzymany przez nas wynik końcowy jest obarczony błędem systematycznym biorącym się stąd, że nie uwzględnialiśmy momentu bezwładności kulki (nie jest ona bowiem punktem materialnym i ma skończone wymiary), nici (która przecież nie jest nieważka i nierozciagliwa, jak to zakładaliśmy) oraz parcia powietrza. Jednak w porównaniu z niepewnością pomiaru g w warunkach naszego laboratorium ten błąd systematyczny jest tak mały, że nie jest celowe uwzględnianie poprawek do wzoru (1). Dyskusja dotycząca błędów systematycznych występujących w tym ćwiczeniu została przeprowadzona poniżej, w Uzupełnieniu.
5. Uzupełnienie
Musimy mieć na uwadze, że wzór (1) ma charakter przybliżony i stosując go godzimy się na popełnienie błędu systematycznego. Jest to uzasadnione jedynie wówczas, gdy niepewność wyznaczenia g, której źródłem będą niepewności pomiaru długości i okresu drgań wahadła, będzie co najmniej o rząd wielkości większa od błędu systematycznego wynikającego z zastosowania wzoru (1) nie uwzględniającego anharmoniczności drgań, rozmiarów kulki jak również szeregu innych czynników jakie tutaj zaniedbaliśmy takich jak: opory powietrza i tarcia wewnętrznego w nitce, siła wyporu powietrza, masa nitki i jej nieznaczna rozciągliwość, fakt, że ruch nie odbywa się dokładnie w jednej płaszczyźnie itp.
Błędy procentowe wyznaczenia g, wynikające z zaniedbania anharmoniczności drgań dla amplitud w zakresie od 1° do 10°, dla kulki o zaniedbywalnych rozmiarach oraz błędy procentowe wyznaczenia g, wynikające z zaniedbania rozmiarów kulki dla wahadeł o stosunku d/l z zakresu od 0,01 do 0,1 podano odpowiednio w tabelach 3 i 4.
Tabela 3
|
.Ml |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
<?[%] |
0,004 |
0,015 |
0,034 |
0,061 |
0,095 |
0,14 |
0,19 |
0,24 |
0,31 |
0,38 |
Tabela 4
|
d/l |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
0,10 |
|
4[%] |
0,002 |
0,008 |
0,018 |
0,032 |
0,050 |
0,072 |
0,098 |
0,13 |
0,16 |
0,20 |
Błędy związane z pozostałymi czynnikami, które wymieniono wyżej są również małe. Dla przykładu, błąd procentowy wynikający z nieuwzględnienia siły wyporu powietrza dla kulki stalowej jest rzędu 0,017%. Charakterystyczne jest to, że wszystkie błędy, o których była mowa mają ten sam znak przez co nie kompensują się wzajemnie. Wszystkie one prowadzą do zaniżenia wartości g. Całkowity błąd systematyczny wynikający z zastosowania przybliżonego wzoru (1) jest, w przybliżeniu, sumą poszczególnych błędów. Jeśli np. zadbamy o to żeby amplituda nie przekroczyła 5°, stosunek średnicy kulki do długości wahadła był nie większy niż 0,02, a kulka wykonana była z materiału odpowiednio dużej gęstości np. ze stali, to błąd procentowy jaki popełnimy stosu-
Wyszukiwarka
Podobne podstrony:
skanuj0004 4 44. Oblicz: a)
skanuj0004 (108) 81 81 otropową ze wzoru (7.5) ni kształtu [ położenia i trunkiem, oo postaci: mm es
skanuj0016 w 1 • 1 kwas 4-hydroksypentanowy, 2-metylobutanal. 2. Korzystając ze wz
skanuj0021 Ćwiczenie 1Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła prostego 1.
skanuj0008 (237) Teoretyczny przyrost naprężeń gnących obliczamy ze wzoru: _AMt APa ^fiiui lt«rcl jy
skanuj0063 (11) 106 B. Cieślar Ze wzoru do obliczenia całkowitego kąta obrotu mamy: 106 B. Cieślar P
skanuj0105 210 b. Obwód z cewką indukcyjną. Korzystając ze wzoru (13) obliczyć induk-cyjność cewki b
26831 skanuj0130 (10) 240 B. Cieślar Naprężenia obliczamy ze wzoru: 240 B. Cieślar 1+ o(x.y)=fl xpx
skanuj0068 136 3. Pomiar 2. Wyznaczyć ru ±Aru w sekundach, a następnie ze wzoru (8) obliczyć wartość
DSC00604 Kąt a* obliczamy ze wzoru : 003= - ao ( 0,44 - 0,005*T *C1) T-temperatura w stopniach Celsj
więcej podobnych podstron