skanuj0079

i n><>1 (i w R\, Ri, Rn, ale także dokładność zrównoważenia mostka oporem Rn-i >|)«nniki użyte w mostku wykonane są z maksymalnymi niepewnościami w/p.lędnymi podanymi w tabeli 6.

Maksymalna niepewność względna zmierzonego opora R_x dana jest wyra-

, cim.-m:

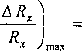
AR, AR-, A Rn AR_n -L +-- +-u_ ₊-CL

/?] R₂ Rn R_n

I )\va pierwsze wyrazy po prawej stronie wypisujemy z tabeli 6, trzeci - dla A'v ■ I O'¹ Q przyjmujemy równy: AR_N/R_n = 3-10^; czwarty mamy wyznaczony i li iświadczalnie (patrz tabela 4).

Tabela 6

Opór [Q]	10^3	“To^2-	10^1	nr	10^_1
Maksymalna niepewność procentowa [%]	±0,03	±0,03	±0,03	±0,1	±0,5
Maksymalna niepewność względna	±3-10'^4	±3-10'^4	±3-10-^4	±M0^-4	±5-10'^3

Maksymalną niepewność względną oporu właściwego liczymy ze wzoru:

Ap]

P Jr

AR, R,

_ Ad Al

+ 2 + —.

d 1

gdzie za Ad i Al podstawiamy niepewności maksymalne tych wielkości.

Na koniec porównujemy ze sobą wartości R uzyskane różnymi metodami oraz otrzymane wartości oporów właściwych drutów p z wartościami tablicowymi.

4. Uzupełnienie

Przewodnikami prądu elektrycznego mogą być ciała stałe, ciekłe (elektrolity) i gazy. Pod względem przewodnictwa elektrycznego ciała stałe dzielimy na:

a) przewodniki; p = (1(T⁸ -r 1(T⁴) Q ■ m,

b)    półprzewodniki; p = (1O^-4    10⁶) fi • m,

c)    izolatory;    p = (10⁶ -s-10¹⁸) Q • m.

Tylko dla metali, które są dobrymi przewodnikami prądu, jest spełnione prawo Ohma (wzór (1)), tj. napięcie jest wprost proporcjonalne do natężenia prądu, a zatem opór elektryczny jest niezależny od napięcia (i?=L^r/J=const).

Dla innych przewodników opór elektryczny definiujemy wzorem: R = i

dl

zależy on od przyłożonego napięcia. Opór elektryczny zależy również od temperatury (patrz ćw.13).

Klasyczną teorię przewodnictwa elektrycznego metali podał Drude, według której elektrony walencyjne traktowane są jak cząstki swobodne podlegające prawom klasycznej statystyki Maxwella-Boltzmanna. Elektrony przewodnictwa zachowują się podobnie jak cząsteczki gazu doskonałego, poruszają się chaotycznie i ciągle się zderzają z drgającymi jonami tworzącymi sieć krystaliczną (zderzenia elektronów między sobą są niezmiernie rzadkie), zmieniając prędkości i kierunki ruchu. Pod wpływem zewnętrznego pola elektrycznego o natężeniu £ chaotyczny ruch elektronów ulega pewnemu uporządkowaniu i przemieszczają się one w kierunku przeciwnym do kierunku pola ze stałą prędkością unoszenia u_e, dając prąd elektryczny. Możemy sobie wyobrazić, że

na poruszające się elektrony oprócz siły pola elektrycznego: F_e = -eE (e -wartość ładunku elementarnego) działa dodatkowo siła hamująca ich ruch, a spowodowana zderzeniami elektronów z drgającymi jonami: Ą_iam =-/?• u_e. Siły te równoważą się wzajemnie:

~jB-u_e=-eE.    (12)

i stąd wartość prędkości unoszenia n_e wyrażona wzorem:

u_e=~E^p_e-E    (13)

jest stała i jest rzędu kilku cm/s. Występujący we wzorze (13) współczynnik p_e nosi nazwę ruchliwości elektronów.

Ładunek zgromadzony w objętości: V = IS przewodnika dany jest wyrażeniem: