Scan10011

Ponieważ SP = SQ oraz SP = *Jx² + y²,SQ =j f(s)\, więc równanie powierzchni oblotowej X?+y² =\f&Y.

Analogicznie równanie powstaje w pozostałych dwóch przypadkach ti. ody krzywa leży w płaszczyźnie XOY lub XOZ. w'ówczas (dla XOY): y² +z² = (/(x)]²

(dla XOZ): x^z +z² = [g-(>’)F, gdzie c jest funkcją odwrotną do f,

U) Tl

RZYKŁAD

“jsoida o równaniu y=sinx obraca się dookoła osi OX. Powstała powierzchnia oplotowa ma równanie:

>³    = sin'x

.'ezei *uk tej samej sinusoidy, dla    obraca się wokół osi OY, to powstała

:: #■ e"2chnia ma równanie :

:    = (arcsłny)'

1 Elipsoida

\a płaszczyźnie XOY leży krzywa o równaniu:

W    I ■

Jest to elipsa. Załóżmy, że a>b i z równania wyliczamy: mb *’

a~    b

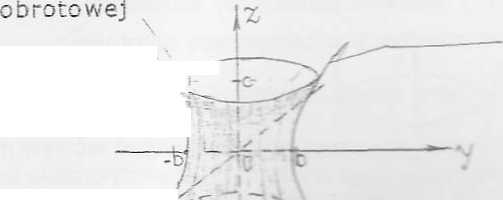
2 Hipe-boioida

'zypuśćmy, że na płaszczyźnie YOZ leży hiperbola o równaniu:

:te :e h perbolę obrócimy dookoła osi OZ to otrzymamy powierzchnię obrotową hiperboloidąjedrnopowłokową.

6wnanie tej powierzchni ma postać:

= y² = b²

f 2 \

ł+^

v Ą

czyli po podstawieniu

■X^2
b^2	b^2 c^2 1

V Y