Scan10054

Całka potrójna

Rozważmy prostopadłościan P określony w przestrzeni OXYZ nierównościami:

a<x<b,    c < y < d, p< z <q

oraz funkcję f(x,y,z) określoną i ograniczoną w tym prostopadłościanie. Ten prostopadłościan dzielimy na „n" prostopadłościanów P_k o objętościach AV_k, k=I,2,...,n. Podział ten oznaczamy

symbolem Ai

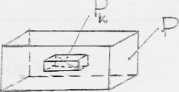
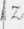
Niech d_k oznacza długość przekątnej prostopadłościanu P_k.

p    t

Liczoę i ~~    nazywamy średnicą podziału Ai. W k

Liczoę i \<t<n ^k nazywamy średnicą podziału Ai. W każdym z prostopadłościanów P, wybieramy dowolny punkt A_k(x_k,y_k,z_k), obliczamy f(A_k) I tworzymy sumę ;

n *« i

Nazywamy ją sumą całkową funkcji f w prostopadłościanie P.

Rozważmy ciąg normalny podziałów (A_n) tzn. taki ciąg dla którego ciąg średnic (5_n) dąży do zera.

0>EFr (całki potrójnej w P)

Jeżeli dla każdego normalnego ciągu podziałów prostopadłościanu P ciąg sum całkow^C.^. -(S_n) jest zbieżny do tej samej granicy- właściwej, niezależnej oc wybory punktów A*, to tę granicę nazywamy całką potrójną w prostopadłościanie P i oznaczamy:

Interpretacja geometryczna ęgłki potrójnej dla_P jeżeli f(x,y,z)=l w P to całka jest równa objętości P.