Scan10039

Całka podwójna po prostokącie

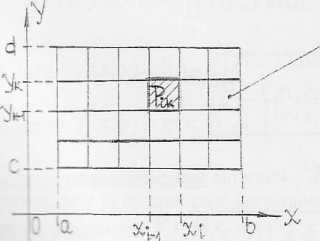
P = {(jc, y): a < x < b, c < y< d)

osz: *cąt ? złożony jest z prostokątów P^:

’ = ! i x. v): x,_j < x < x_t,y_t__l < y < y_k}, powstały w wyniku podziału Pi_: mecz erj < ^,b >: a = x₀ < x, <... <    = b

mecz-aru <c,a>:c= v₀ < >’j <... <y^-d _m

1* - pole prostokąta P|_k, e d,_k - jego przekątna.

MJM II BP¹!¹ I

•iajdruzszą przekątną oznaczamy

^-• ⁼ ® to ciąg podziałów nazywamy normalnym (n co prostokąta).    '

średnica podziału Pi. jeżeli fen., że zagęszczamy podział

w Pm wybieramy (£/»7*) i dla niego mamy j£(5»%) (/(*»}') -ograniczona w P). wówczas iloczyn f(4t*Voznacza objętość bryły o podstawie ^7- .Utwórzmy sumę:

*

V

*=1

DEF,    sO-

jeżeli istnieje skończona granica

Jjjjż Ź

i=l A=1

niezależnie od wyboru punktów Osp7*) i przy normalnym ciągu podziałów P to nazywamv ją całką, podwójną po prostokącie P i oznaczamy: 1

-b