Strona0204

9. DRGANIA GIĘTNE

9-1. Równania ruchu. Częstość własna

Drgania układu mechanicznego nazywamy giętnymi, jeżeli elementy sprężyste są zginane w czasie drgań. Siły sprężyste w tym przypadku sprowadzą się do par, których momenty są równe momentom zginającym. Drgania giętne mogą wykonywać belki, wały, płyty itp. Towarzyszy im pewien hałas oraz drgania podstaw łożysk. Drgania giętne są uzależnione od wzajemnego oddziaływania sił oraz par sił wewnętrznych i zewnętrznych.

W miarę postępu w budowie maszyn wzrastała stopniowo potrzeba wyznaczania krytycznych częstości drgań giętnych wałów oraz dokładnego wyważania ruchomych części elementów maszyn 1 silników.

W związku z układami wirującymi występują również inne zagadnienia, mianowicie: usztywniające działanie wirników o dużych średnicach, zjawiska spowodowane tarciem i krążeniem smaru łożyskowego czy wreszcie drgania giętne wałów nieokrągłych.

Dziedzina drgań giętnych jest bardzo obszerna i wobec tego możemy podać tylko główne jej podstawy oraz wskazać niektóre najważniejsze problemy.

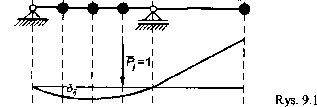
Rozpatrzymy drgania swobodne dowolnie zamocowanej belki, mającej skończoną liczbę skupionych mas (krążków) mi, m₂,m„ (rys. 9.1). Wcześniej podano dla takiego przypadku odwrotną postać równań mchu, polegającą na wprowadzeniu sił bezwładności przyłożonych do bezmasowego sprężystego modelu układu mechanicznego. W tym celu wygodnie jest korzystać z tzw. współczynników wpływu znanych z kursu wytrzymałości materiałów. Współczynniki te możemy wyznaczać z linii ugięcia belki będącej pod działaniem siły jednostkowej lub też ze wzoru Mohra albo Wereszczagina.

I m,I m₂I m₍-l I    mj