Strona0052

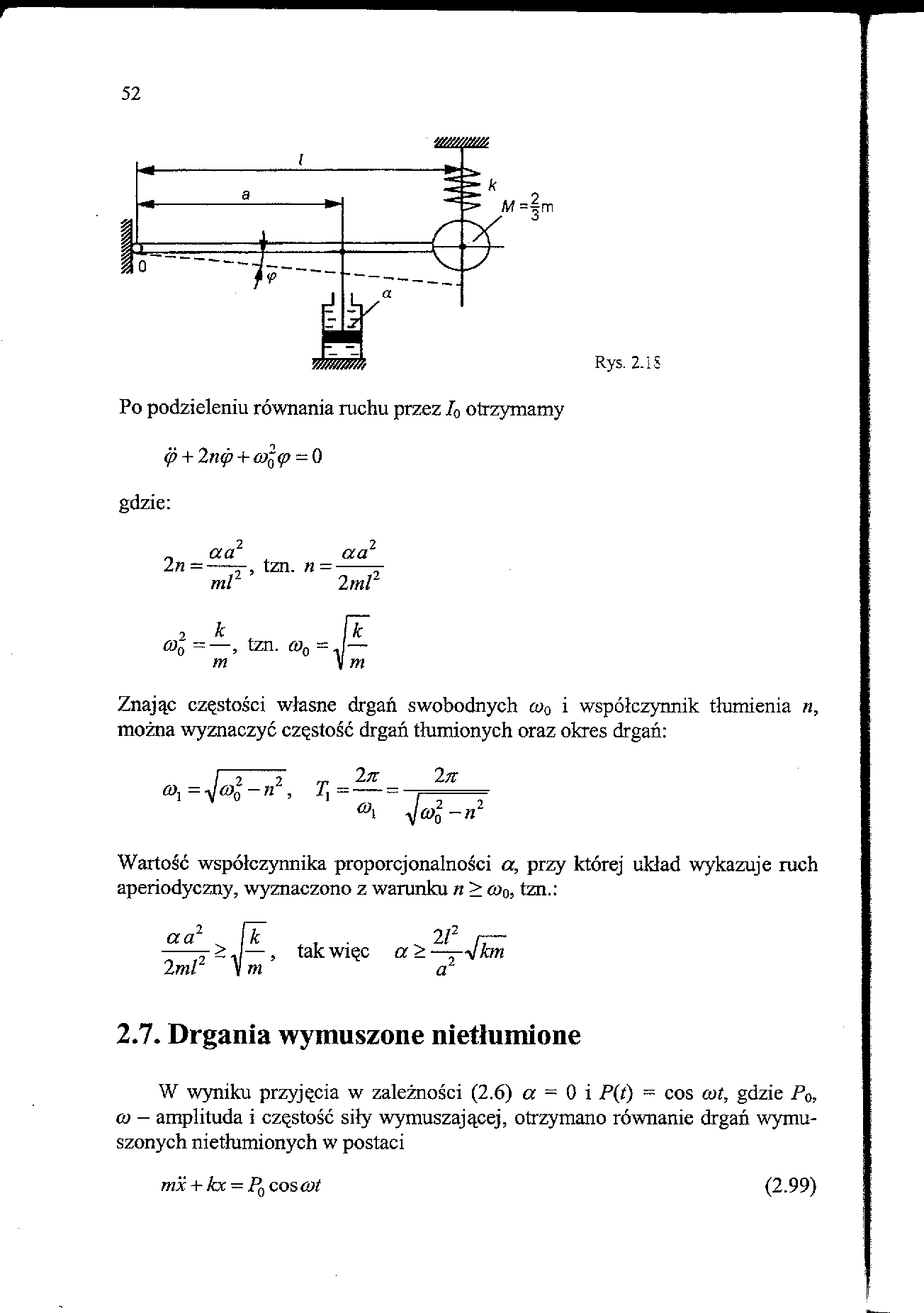
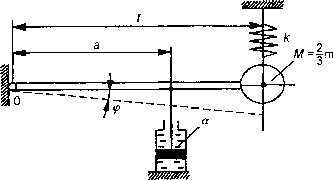
Po podzieleniu równania ruchu przez 7₀ otrzymamy ę + 2nę + gj>q (p - 0

gdzie:

aa^22 n-—=-ml^1	, tzn. n =	er u^2
		2m/^2
2 * m	tzn. co0 =.	£

Znając częstości własne drgań swobodnych co₀ i współczynnik tłumienia n, można wyznaczyć częstość drgań tłumionych oraz okres drgań:

27t _    2jt

-«²

Wartość współczynnika proporcjonalności a, przy której układ wykazuje ruch aperiodyczny, wyznaczono z warunku n > <o₀» tzn.:

-y £ J—, tak więc a >

2ml² V m    u²

2.7. Drgania wymuszone nietłumione

W wyniku przyjęcia w zależności (2.6) a - 0 i P(i) = cos rot, gdzie To, cy - amplituda i częstość siły wymuszającej, otrzymano równanie drgań wymuszonych nietłumionych w postaci

(2.99)

mx + kx = P_a cos a?t