Slajd38 2

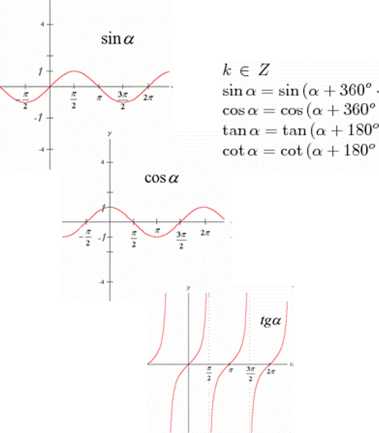
Funkcje parzyste: cos(—a) = cos a Funkcje nieparzyste:

sin(—a) = — sina tan (—a) = — tana cot(—a) = — cot a

Trygonometria płaska

■ P s a + (3 —)-cos——

Wzory na różnice funkcji trygonometrycznych

sin q — sin /? = 2 sin (-cos a — cos f3 - —2 sin (-

tan a — tan (3 -cot a — cot {3 =

sin (a — P) cos a • cos P sin (P — a) sin ol • sin P

cos ol — sin a = \/2 cos (— 4- a) = y/2 sin (-— a)

4    4

sin² ot — sin² P = cos² p — cos² a = sin (a + /?) • sin (a — p) cos² a — sin² P = cos² p — sin² a = cos (a -ł- P) • cos (a — /?)

Wzory na sumy funkcji trygonometrycznych

,    • o o •    +

sin q +■ sin p = Z sm( —-—) • cos( —-—)

OL + P\ .Ol — P

cos oc 4- cos P = 2 cos( ———) • cos( —-—)

sin(a + /?)

tan q -f tan p = --

COS Q • COS P

sin (f3 + a)

cot a 4- cot p = —-_:——

sin a • sin p

cos ol 4- sin a = \/2 sin (— 4- a) = \/2 cos (-— a) 4    4