WM015

skąd, pomijając wielkość nieskończenie małą trzeciego rzędu*⁰, otrzymujemy zależność

t_xz = r_zx    [9-22]

wyrażającą prawo równości naprężeń stycznych zbiegających się na krawędzi rozpatrywanego prostopadłościanu.

A zatem naprężeniom stycznym r_xz w przekrojach poprzecznych belki towarzyszą naprężenia styczne r_zx, występujące w przekrojach podłużnych równoległych do powierzchni obojętnej. Naprężenia r_zx stają się zerami na dolnej i górnej powierzchni belki (o ile nie ma na nich obciążeń stycznych). Wynika stąd wniosek, że w przekrojach poprzecznych przy górnej i dolnej krawędzi naprężenia styczne są równe zeru, a zatem rozkład naprężeń stycznych na wysokości przekroju nie może być liniowy.

9.3.2

Naprężenia styczne w belkach o przekroju prostokątnym

W celu przeanalizowania rozkładu i wartości naprężeń stycznych w przekroju poprzecznym belki odetnijmy od elementu belki pokazanego na rys. 9-9c, przekrojem 3-3 w odległości z od powierzchni obojętnej, równolegle do niej, dolną część

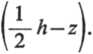
Fragment

w postaci prostopadłościanu o podstawie bdx i wysokości

ten pokazany jest na rys. 9-9d wraz z działającymi nań naprężeniami, wyrażającymi oddziaływania sąsiednich części belki.

Na ścianach bocznych: lewej a₁d₁d[a[ i prawej a₂d₂d'₂a'₂ w odległości f od osi

obojętnej, zawartej w granicach — ^    ^ z, panują naprężenia normalne, które

zgodnie z nadal obowiązującym wzorem [9-8] wynoszą odpowiednio

a —

MaC_

J,

oraz

a+da —

(M_a+dM_a)C

Jy

A zatem na lewą ścianę prostopadłościanu działa siła normalna równoległa do osi x

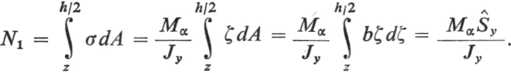
Analogicznie na prawą ścianę działa

A/2    h/2    1,12

₌ M_a+dM_a P ₌ (.M_a+dM_a)S_y

J y    J    Jy

N₂ = J (i<r+da)dA =

M_a + dM_a

CdA