0000049 2

W tya sformułowaniu

^c'^,x>

Dysponujęc metodę wyznaczania optymalnego kolorowanlo 1 liczby J-(G) motoay wyznaczyć liczbę podzielności dowolnago grafu, korzystając z następującego twierdzenia.

TWIERDZENIE 6.1

Liczba podzielności p(G) dowolnego grafu C Jest równa liczbie chromatycznej t(G_#) szkieletu tego grafu C_t.

Teza twierdzenia wynika bezpośrednio z definicji użytych pojęć.

6.2.1. Algoryte optymalnego kolorowania wierzchołków

grafu

Każdy podzbiór maksymalnego zbioru wewnętrznie stabilnego joot zbiorem wewnętrznie stabilnym. Zatem wozyetkle zbiory wewnętrznie stobilne danego grafu (hlpergrafu) G - <X,U,P> określa zbiór wszyotklch maksymalnych zbiorów wewnętrznie stabilnych.

.V punkcie 6.1 został opisany eposób wyznaczanie wszystkich pokryć minimalnych. Potrafimy zatem wyznaczyć wozystlie minimalne pokrycia zbioru X maksymalnymi zbioroml wewnętrznie etabll-nymi.

Zauwużmy więc, że dle każdego minimalnego pokrycia zbioru X maksymalnymi zbiorami wewnętrznie otabllnyml, możemy wyzna -czyć przynajmniej Jeden minimalny podział w sposób naatępujęcyt

Niech {Xj.....X_r) tworzę pokrycie. Zbiory (Aj.....A_fJ

tworzęce podział określamy następujęco (patrz ryo.6.1)

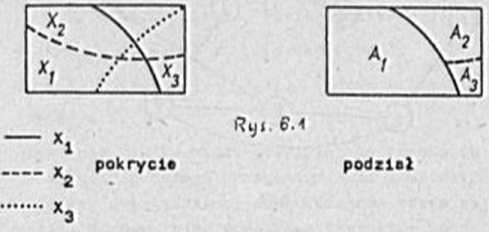
^ * V*2 ' ™₂\ *1'^3 * *₃\ (*1^*2)....

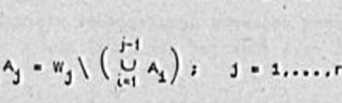
Przeprowadzone rozważania stonowlę podstawę algorytmu wyznaczania wazyetklch optymalnych kolorowoó wierzchołków dowolnego grafu bez pętli.

O)

Procedura tago algorytmu okłada elę z trzach zasadniczych etapów j

1° Znajdujemy wszystkie aakoyaalna zbiory wewnętrznie atebllno x_k (patrz algorytm wyznaczania wazyetklch baz minimalnych). 2° Znajdujemy wozyatklo minimalne pokrycia zbioru X, zbiorami X_k (patrz algorytm oplaany w punkcie 6.1).

3° Spośród pokryć minimalnych wybieramy dowolne pokrycie naj-oniej liczna 1 tworzycy z niego podział zbioru X na pod -zbiory    i • 1,..., y(C).

wierzchołkom x należęcym do tego samego podzbioru Aj przy-porzydkowujeay barwę o numerze i. w tan apoeób c* (x) ■

■ 1H Xi Aj.

Przykład 6.1

Realizacja pewnego przedsięwzięcia wymaga wykonania eled-alu prac. Czas wykonywania każdej pracy trwa Jeden dzień. Ze względów technologicznych niektóro prace nie mogę być wykonywane Jednocześnie (w tym samym dniu). Należy tak zaplanować har-aonograa wykonywania prac, aby zużyć najeniajazę ilość dni na wykonania całego przedsięwzięcia. Modelem systemowym obiektu zainteresowań Jert graf zwykły C • <X,U,P> przedstawiony na rys.6.2. gdzie wierzchołki x( X reprezentuję prace do wykona -nie. a krawędzie łęczę ta praca, która nie mogę być jednocześnie wykonywana.

Nietrudno zauważyć, że rozwlęzanle zadania sprowadza się do wyznaczania optymalnego pokolorowania wierzchołków grafu C.

97