019(1)

3) Jeżeli x -» O, to ^ -» oo i arc tg nie dąży do żadnej określonej

wartości, czyli lim arc tg ¹ = arc tg oo nie istnieje.

*-»o    ^x

Wykres tej funkcji podano na rys. 19.

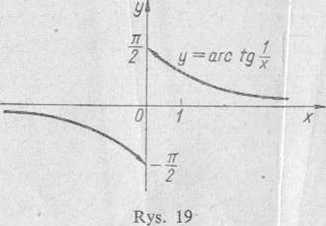
34. Wyznaczyć granice- funkcji y — 3^tgx; gdy: l)x-»    — 0,2) x -* ^+0,

Rozwiązanie

1) Gdy x -> ", —0(w pierwszej ćwiartce), to tg o^- -» 4- co, a więc funkcja 3^lBX -> -f oo, co oznacza, że jest ona wielkością nieskończenie wielką:

oo.

lim 3‘^ex = 3+* =

2) Gdy x -» ” -1- O (w drugiej ćwiartce), to tg x -> — ooy a więc funkcja 3'b* o, czyli jest wielkością nieskończenie małą: lim 3^,8X = 3 * = O

3) Gdy x — y w dowolny sposób, t® tg x -* oo, przyjmując wartości zarówno dodatnie jak i ujemne. Dlatego, gdy x - -^.funkcja 3^{ls x} nie ma granicy i nie jest też wielkością nieskończenie wielką. Zatem lim 3*^{3 x} =

nie istnieje.

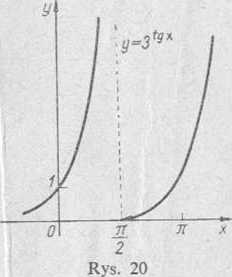
Wykres tej funkcji został przedstawiony na rys. 20.

35. Biorąc n = 1, 2, 3, ...ułożyć tabelkę odpowiednich wartości zmiennych: a, = 2", a₂ = —2", a₃ = ( 2)", a₄ - 2"", rr₅ = -2"", ot* = ( 2)“" oraz scharakteryzować zachowanie się tych zmiennych, gdy n -* -(- oo.

36. Biorąc n — 1, 2, 3. ... napisać ciągi wartości zmiennych: X = —j,

/ _nn n    ( —1)"4-3n    3ncosnrr    . nn .    ..,

fl "T 2

y — (-1)- ^z = - A,—» M =    , f = 2 sin— t ustalić,

które z tych zmiennych mają granicę, gdy n -» + co, oraz podać jej wartość.

37.    Wykazać, że:

1) lim (3.v- 2) = 1    2) lim (a² j-3) — 7    3) lim (x² — 3x) = 0

x >!    x-*—2    x~>3

„ ,.    3x— 2    3    2x²+l

4) hm -    - -    5) lim , = -2

a:-* oo —^    .y > oo    ^A

38.    Wyznaczyć granice:

3) lim-_T

x—3

JL    _L    _ł

4) lim 3*^fl 5) lim 3^X+1    6) lim 3*"

x->—1 — 0    x-*- — 1 + 0    x-+— 1

1) lim —- _    2) lim ——

x >3—0 X — 3    ,v-*3 : 0 X — J

Zilustrować rozwiązania tabelkami.

Rys. 21

39. Odcinek AB o długości / podzielono na n równych części (rys. 21) i na każdej z nich (wyłączywszy skrajne) zbudowano trójkąty równoboczne. Jak będzie zmieniać się pole S„ i obwód P„ otrzymanej zębatej figury, gdy « -> + cp.

37