062(1)

Maclaurina dla funkcji sin* też dąży do zera dla dowolnej wartości x, czyli

lim R_2m = 0

m-^j*-+ oo

Pokazaliśmy więc, że dla każdej wartości x możemy funkcję sin* zastąpić wielomianem Maclaurina, przy czym błąd może być dowolnie mały. Stopniowe zmniejszanie błędu osiągamy biorąc coraz to większą ilość wyrazów wielomianu aproksymująćego.

Biorąc kolejno m = 1, 2, 3,- otrzymamy najprostsze przybliżone wzory dla sin*

sin * ~ *

x³

sin * x x— 7-6

^smJt~*-‘T ⁺ T20

Drugi z tych wzorów jest dokładniejszy od pierwszego, a trzeci jest dokładniejszy od drugiego.

3) Funkcja cos* i jej pochodne mają dla * = 0 następujące wartości

Pochodne rzędu nieparzystego dla * = 0 są równe zeru, zatem w wielomianie Maclaurina, przybliżającym daną funkcję, wystąpią tylko parzyste potęgi *

*² x⁴

^cos*~ ^~2T + 1T^-

*

6l

X²"¹

(2m)\

(3)

/(*) = cos*	/(O) = 1
/'(*) = - sin,* = cos |x+ -~-j	/'(O) = 0
/"(*) = — cos * = cos |*-f2---^-|	/"(0) = -1
/"'(*) = sin x = cos |*+3 • |	/'"(O) = 0
f^(k)(x) = cos 1*4-k • j	/<*>(()) — cos A' y

Otrzymana przybliżona równość wyraźnie uwidacznia, że funkcja cos* jest funkcją parzystą, tj., że cos(—*) = cos*.

Błąd przybliżenia wynosi

^R2m+l = (2*! +2)! ^cosp^jc+(¹^ + ¹) yj > 0<0<1

Uwalniając się, na mocy nierówności |cosa \<U od niewiadomej 0 otrzymamy nierówność

^2m + 2

^^2,n+1i ^ (2m+2)!

która pozwala na łatwe oszacowanie błędu, wynikłego przy zastąpieniu funkcji cos* wielomianem (3).

Badając zachowanie się błędu R_2m+; dla różnych wartości * przy m-* +oo (za pomocą tych samych rozw'ażań co w poprzednich dwóch zadaniach), dochodzimy d<5 następującego wniosku: dla dowolnej wartość *, gdy m -*• +co, Rzm+i we wzorze Maclaurina dla funkcji cos* dąży do zera, czyli

lim    — 0

HI—00

Wynika z tego, że dla każdej wartości * funkcję cos* można przedstawić w sposób przybliżony za pomocą wielomianu Maclaurina z dowolną zadaną dokładnością, przy czym coraz to większą dokładność przedstawienia uzyskujemy przez zwiększenie ilości wyrazów wielomianu aproksymu-jącego (3).

Biorąc kolejno m = 1, 2, 3, otrzymamy najprostsze przybliżone wzory dla funkcji cos*, wg rosnącej dokładności

1 z¹

cos xx 1--—-

cos * x

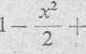
24

cos * X

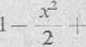
24

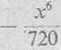
(* jest miarą łukową kąta).

303. Funkcje: 1) x^m oraz 2) ln* przedstawić w przybliżonej postaci wielomianami stopnia n względem dwumianu *—1 i oszacować błąd. Następnie podstawiając / = *—1 napisać rozwinięcia tych funkcji względem potęg t.

127

1